Экзаменационные задачи по дисциплине "Теоретические основы электротехники", 3-я часть – электромагнитное поле (с ответами), страница 7

Решение. При включении тока  в обмотке w и возникновении магнитного потока Ф, замыкающегося по ярму Я, полюсным наконечникам П и ротору Р, выполненным из стали, на последний действует момент, стремящийся повернуть ротор вокруг оси 0 – 0. Для определения этого момента необходимо выражение для энергии магнитного поля двигателя продифференцировать по углу a, определяющему положение ротора. При этом с целью облегчения последующих расчетов выберем в качестве этого угла угол a, опирающийся на дугу перекрытия цилиндрических поверхностей полюсных наконечников и ротора.

Энергию магнитного поля двигателя рассчитаем через индуктивность обмотки, которую запишем в виде:

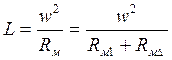, где R_м1, R_мD - магнитные сопротивления, соответственно, участков магнитопровода и воздушных зазоров между полюсными наконечниками и ротором. Не претендуя на высокую точность расчета, пренебрежем магнитным сопротивлением R_м1 путей магнитного потока по стальным участкам магнитопровода (ярмо, полюсные наконечники и ротор) по сравнению с магнитным сопротивлением R_мD воздушных зазоров и тем самым упростим выражение для индуктивности 

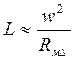, причем для суммарного магнитного сопротивления двух воздушных зазоров имеем

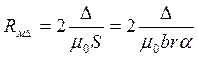, где S – площадь перекрытия полюсных наконечников и ротора, D - длина каждого зазора, r – средний радиус ротора и расточки полюсных наконечников, b – толщина магнитопровода (рис.1).

Таким образом, для энергии магнитного поля двигателя имеем

.

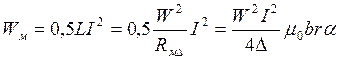Выполняя дифференцирование при условии постоянства токов, для момента реактивного двигателя получим

.

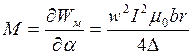Положительный ответ показывает, что момент стремится увеличить угол a, т.е. стремится повернуть ось ротора до совпадения с осью полюсов.

Билет №31. Определить силу, втягивающую конический стальной сердечник в отверстие ферромагнитной плиты (рис.1), если магнитный поток в сердечнике равен Ф. Магнитная проницаемость сердечника и плиты велика ().

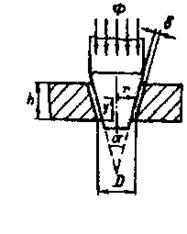
Рис.1

Решение. Напряженность поля в зазоре, аналогично предыдущей задаче, всюду одинакова. Выразим ее через поток. Две горизонтальные плоскости, проведенные на расстояниях y и y + dy от нижней поверхности плиты, вырезают на поверхности конуса элементарную площадку

.

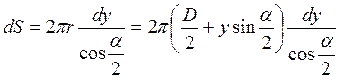Магнитный поток

.

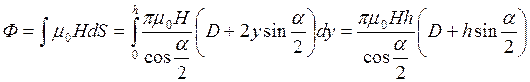Сила, действующая на боковую поверхность конуса, равна:

.

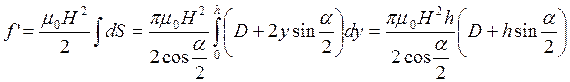Выражая Н через Ф, определяем силу, втягивающую сердечник

.

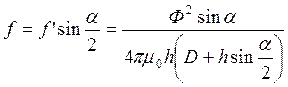Билет №32. Рассчитать магнитную цепь, изображенную на рис.1. Магнитную проницаемость считать постоянной.

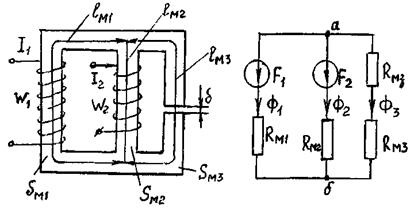
Рис.1

Решение. На рис.1,б изображена схема, соответствующая магнитной цепи (рис.1,а). Направления МДС и величины магнитных сопротивлений определяются аналогично тому, как это сделано в предыдущей задаче.

Поскольку магнитная цепь сложная (два источника МДС), рассчитываем цепь методом узловых магнитных напряжений. Принимаем скалярный магнитный потенциал точки б - , тогда магнитное напряжение между точками  и б -  = .

_.

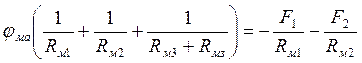Определив из последнего выражения величину j_ма, можно найти магнитные потоки в стержнях магнитной цепи.

;         ;        .

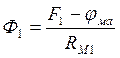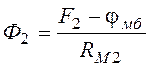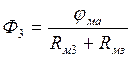Билет №33. Рассчитать магнитную цепь, изображенную на рис.1,а, если зависимость В(Н_с) нелинейна (рис.2).

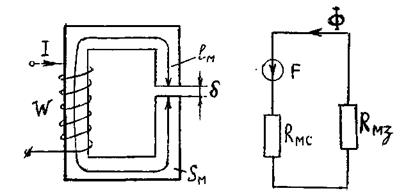
Рис.1

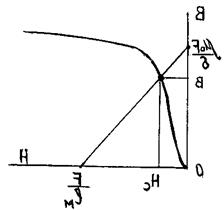
Рис.2

Решение. Второй закон Кирхгофа для магнитной цепи рис.1,а

.

Поделим все слагаемые последнего выражения на l_м:

.

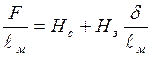На рис.2 построена зависимость В(Н_с), соответствующая этому уравнению:

Н_з = 0 (что соответствует В = 0, т.к. В = m₀Н_з);  Н_с = .

Н_с = 0; 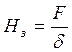  (что соответствует  В = m₀Н_з = ). 

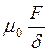Через две точки строим прямую В(Н_с).

На пересечении двух кривых: только что построенной прямой и заданной кривой намагничивания определяем искомые значения В и Н_с; Н_з = .

Билет №34. Возьмем тороидальный сердечник из магнитотвердого материала и сделаем в нем распилы. Намотаем на него обмотку и пропустим по ней постоянный ток. После этого ток выключим и обмотку смотаем. Часть сердечника между двумя распилами вынем (рис.1,а) – получим постоянный магнит. Определить значение магнитной индукции постоянного магнита. Зависимость В(Н_с) магнитотвердого материала изображена на рис.1,б.