Билет №9. Прямолинейный
длинный изолированный провод, по которому протекает ток I
= 60A, расположен в воздухе параллельно плоской
поверхности стальной плиты на расстоянии h = 2см от нее
(рис.1). Относительная магнитная проницаемость стали ![]() .
Требуется найти напряженность магнитного поля в точках
.
Требуется найти напряженность магнитного поля в точках ![]() и
и
![]() . Координаты точек
. Координаты точек ![]() и
и
![]() :
: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
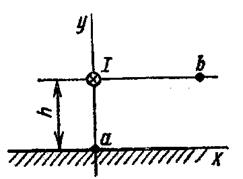
Рис.1
Решение. Воспользуемся методом зеркальных изображений. Найдем фиктивный ток I2 (рис.2):
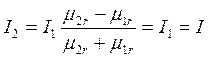 .
.
В силу симметрии напряженность
магнитного поля в точке ![]() -
- ![]() . Напряженность магнитного поля в точке
. Напряженность магнитного поля в точке ![]() -
-![]() , где
, где
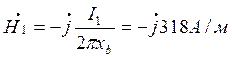 ;
;
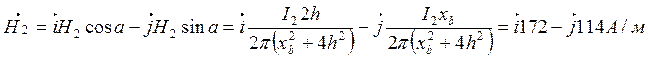 .
.
Окончательно получим
![]() , где
, где ![]() ,
, ![]() - единичные орты вдоль осей x и y.
- единичные орты вдоль осей x и y.
|
|
Рис.2
Билет №10. Определить
напряженность магнитного поля на оси цилиндрической катушки с током I. Длина катушки l,
средний ее радиус ![]() , число витков
, число витков ![]() (рис.1).
(рис.1).
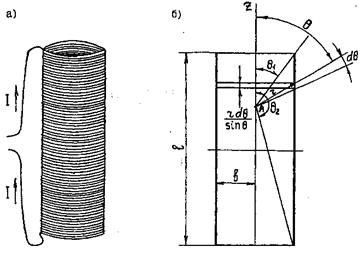
Рис.1
Решение.
Цилиндрическая проволочная катушка, изображенная на рис.1,а, обычно
называется соленоидом. Предположим, что обмотка соленоида распределена вдоль
его длины плотно и равномерно, так что число витков обмотки на 1 м длины
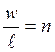 . И хотя в действительности ток идет по
спирали, но если витков много и они расположены плотно друг к другу, можно этим
пренебречь и рассматривать соленоид как совокупность колец с током.
. И хотя в действительности ток идет по
спирали, но если витков много и они расположены плотно друг к другу, можно этим
пренебречь и рассматривать соленоид как совокупность колец с током.
Рассмотрим сначала вклад кольца с током, расположенного между радиусами, проведенными из т. А на оси z и образующими с осью z углы q и q + dq (т.е. определим напряженность поля в произвольной точке А на оси соленоида от названного кольца). Длина рассматриваемого кольца, выделенного на рис.1,б,
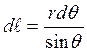 .
.
По этому кольцу протекает ток 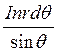 . Напряженность поля от этого тока в
произвольной точке А
. Напряженность поля от этого тока в
произвольной точке А
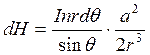 .
.
Подставляя в это выражение 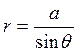 , найдем
, найдем
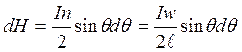 .
.
Интегрирование в пределах от q1 до q2 дает
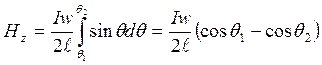 .
.
Для бесконечно длинного соленоида
(а практически при 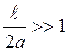 ) q1 = 0, q2
= p, поэтому
) q1 = 0, q2
= p, поэтому
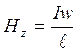 .
.
Опыт и расчет показывают, что чем длиннее соленоид, тем меньше напряженность поля снаружи него. Для бесконечно длинного соленоида магнитное поле снаружи отсутствует вообще. Это также видно из последнего выражения: магнитодвижущая сила Iw полностью уравновешивается магнитным напряжением Hzl внутри соленоида.
Полученные результаты можно распространить и на тороид. Вне тороида, т.е. за пределами обмотки тороида (как снаружи «бублика», так и внутри) Н = 0. На оси тороида
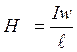 .
.
Билет №11. Катушка
намотана в виде плоской спирали (рис.1) из большого числа w
плотно уложенных витков, по которым течет постоянный ток I.
Радиусы внутреннего и внешнего радиусов витков равны ![]() и
b. Найти напряженность поля в центре катушки –
точке О.
и
b. Найти напряженность поля в центре катушки –
точке О.
|
|
Рис.1
Решение. Вклад в результирующую напряженность от одного витка радиуса r
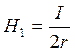 .
.
От всех витков
![]() , где dw
– число витков в интервале (r, r + dr),
, где dw
– число витков в интервале (r, r + dr),
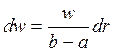 .
.
Подставив значения Н1 и dw в выражение для Н, найдем
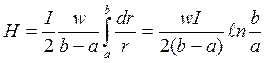 .
.
Билет №11. Требуется
рассчитать магнитное поле внутри, вне и в стенке ферромагнитной трубы,
находящейся во внешнем однородном поле с индукцией В0 (рис.).
Проницаемость материала трубы ![]() . Определить коэффициент
экранирования
. Определить коэффициент
экранирования ![]() , где В1 -
индукция внутри трубы.
, где В1 -
индукция внутри трубы.
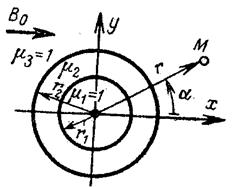
Рис.1
Решение. Так как в
рассматриваемом объеме отсутствуют токи, то ![]() и МП
потенциально. Вводя функцию скалярного магнитного потенциала (
и МП
потенциально. Вводя функцию скалярного магнитного потенциала (![]() ) и применяя круговые цилиндрические
координаты, решение уравнения Лапласа для
) и применяя круговые цилиндрические
координаты, решение уравнения Лапласа для
jм можно представить в виде (выбирая jм = 0 при r = 0):
1) 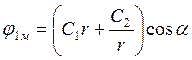 при
r £ r1;
при
r £ r1;
2) 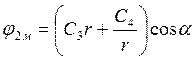 при
r1 £ r £ r2;
при
r1 £ r £ r2;
3) 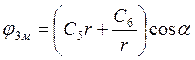 при
r ³ r2;
при
r ³ r2;
Так как при r = 0 поле должно оставаться конечным, то С2 = 0.
Труба заметно искажает внешнее однородное поле в точках, находящихся вблизи трубы. Вдали от трубы (r ® ¥) ее искажающее действие будет незаметно, и поле останется однородным, т.е. H = Hx = H0 и j3м = - H0x = -H0rcosa. Отсюда следует, что С5 = -Н0.
Остальные четыре постоянные определяются из граничных условий при а) r = r1 и б) r = r2.
а) j1м
= j2м и ![]() ;
;
 и
и 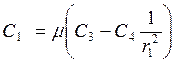 ;
;
б) аналогично
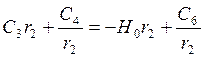 и
и 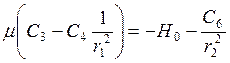 .
.
Совместное решение четырех уравнений дает:
![]() ;
; ![]() ;
; ![]() ;
; ![]() , где
, где 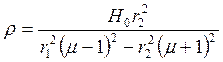 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.