Оптимизация бизнес решений на базе использования средств электронных таблиц: Учебное пособие по дисциплине «Модели и моделирование на транспорте», страница 2

Для отражения условий модели и выражения целевой функции воспользуемся математической функцией Excel,  СУММПРОИЗВ, которая рассчитывает сумму произведений чисел, размещенных в двух и более массивах. Для целевой функции поместим: B2= СУММПРОИЗВ(C2:F2,C3:F3). Для левых частей ограничений (2) постановки задачи в клетках H4:H8 зададимся:

H4= СУММПРОИЗВ($C$3:$F$3,C4:F4)

H5= СУММПРОИЗВ($C$3:$F$3,C5:F5)

H6= СУММПРОИЗВ($C$3:$F$3,C6:F6)

H7= СУММПРОИЗВ($C$3:$F$3,C7:F7)

H8= СУММПРОИЗВ($C$3:$F$3,C8:F8)

Остальные части формы предназначены для анализа  оптимального плана, и мы к ним вернемся по мере необходимости позже.

После подготовки форм перейдем к построению оптимального плана. Войдем в меню Excel,

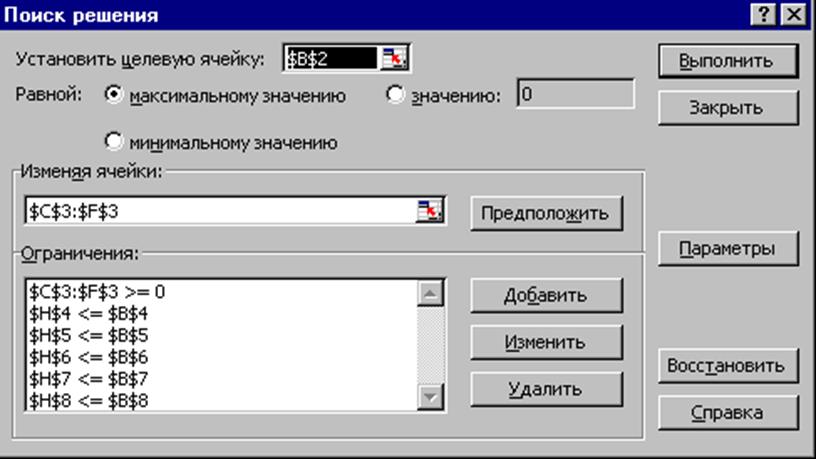Рис1. Диалоговое окно Поиск решения выберем Сервис и в нем Поиск решения. Открывается диалоговое окно Поиск решения – рис1. В

поле Установить целевую ячейку занесем адрес клетки функции F, т.е. адрес $B$2. Установим переключатель целевой функции в положение Максимальному значению. В поле Изменяя ячейки  установим диапазон клеток,  отражающих переменные $C$3:$F$3 - базиса плана задачи. В поле Ограничения введем условия постановки, используя кнопку Добавить. Появляется диалоговое  окно Добавление ограничения. Введем в левое поле Ссылка на ячейку ограничение по левой части для ресурсов А1: $H$4. Переключателем  установим тип ограничения на ”<=”.Введем в правое  поле Ссылка на ячейку ограничение по ресурсам  $B$4. Аналогичным образом через кнопку Добавить введем ограничения по А2, А3, А4, А5 для клеток H5:H8 и  сответственно B5:B8. Занесем условие неотрицательности переменных x_j>=0: $C$3:$F$3>=0.

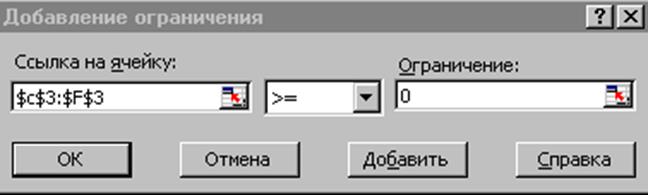Рис2. Диалоговое окно Добавление ограничения

Если нужно скорректировать  выражения для ограничений или удалить их  можно воспользоваться соответствующими кнопками  диалогового окна Изменить  или Удалить.

Рассмотрим теперь возможности изменения режимов решения задачи. Для этого в  окне Поиск

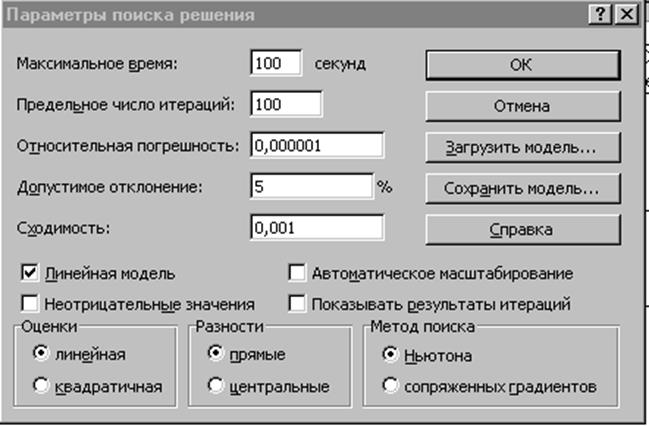Рис. 3. Диалоговое окно Параметры поиска решения

решения нажмем кнопку Параметры.  Появляется окно Параметры поиска решения-см. рис 3.

Определим режимы расчета задачи линейного программирования

Оценка	Разности	Метод поиска
Линейная	Прямые	Ньютона

Выйдем из окна Параметры поиска решения через кнопку ОК. В окне Поиск решения нажмем кнопку Выполнить. Скоро появляется Результаты поиска решения.

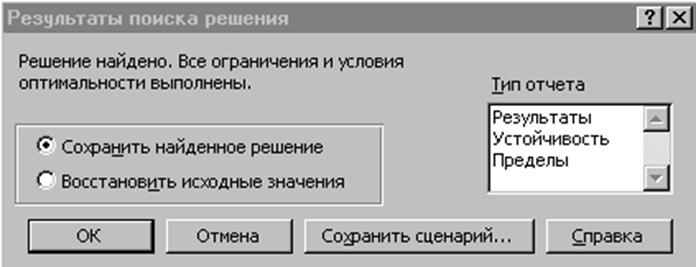Рис. 4. Диалоговое окно Результаты поиска решения

Если математическая модель корректна и форма ввода условий постановки задачи введена правильно, в этом окне появляется сообщение: Решение найдено. Все ограничения и условия оптимальности выполнены. Принимаем по умолчанию сообщение Сохранить найденное решение. Кнопка ОК.

Если задача не имеет решения могут быть два вида сообщений в окне Результаты поиска решения: в случае несовместных условий постановки сообщение Поиск не может найти подходящего решения; если целевая функция не ограничена, Значения целевой ячейки не сходятся.  В нашем случае (если все сделано верно) должна появиться форма1.2.

Аналитическая таблица: Оптимальный план выпуска.      форма1.2.