Деталі машин: Конспект лекцій № 1-11 (Зварні з'єднання. Муфти приводів), страница 19

:

Тут: α - кут обхвату ременя;

β -кут пружного ковзання ременя;

f - коефіцієнт тертя ременя по шківу;

l - основа натуральних логарифмів.

Тому що натяг гілок ременя неоднакове, то й відносне подовження їх за законом Гука також буде неоднаковим. На дузі β ці подовження вирівнюються, що може мати місце лише за умови пружного ковзання ременя, величина дуги β залежить від переданого навантаження. Якщо навантаження увесь час збільшувати, то в межі дуга  досягне дуги α Фізично це буде відповідати повному буксуванню ременя, що зовсім неприпустимо. Відносне подовження гілок ременя:

; .

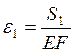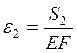Відносне пружне ковзання ременя:

.

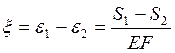Пружне ковзання ременя під навантаженням цілком закономірно, воно звичайно не перевищує 0,02 (2%);  якщо передачу перевантажити, то пружне ковзання переходить у неприпустиме буксування.

Сили, що діють у пасовій передачі

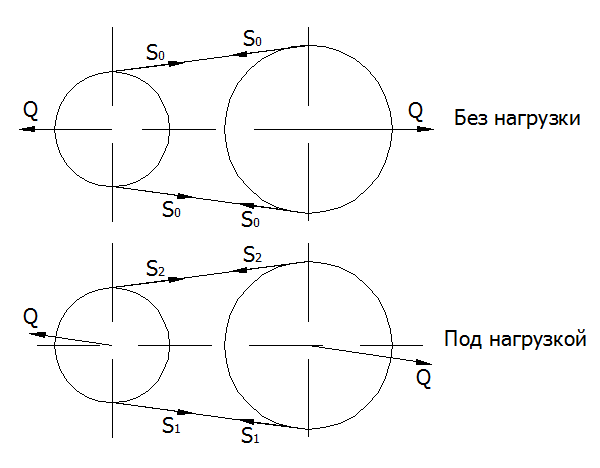
Рис .54

1. Окружне зусилля .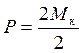

2. Зусилля попереднього натягу гілок ременя - S₀ 

3. Зусилля натягу гілок ременя в роботі. На основі рівноваги гнучкої нитки:

Теорема Понселе: Сума зусиль натягу гілок ременя в стані спокою й руху під навантаженням є величина постійна:

Наслідок теореми Понселе: При переході від стану спокою до стану роботи під навантаженням зусилля гілки, що набігає, збільшується на величину половини окружного зусилля, зусилля що збігає - на стільки ж зменшується.

; 

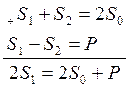
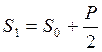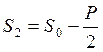
4. Навантаження на вали й підшипники:

;   .

Коефіцієнт тяги й криві ковзання ременя

Коефіцієнтом тяги називається відношення корисного окружного зусилля до повного зусилля натягу галузей ременя.

По фізичному змісті коефіцієнт тяги характеризує ступінь завантаження передачі:

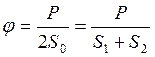
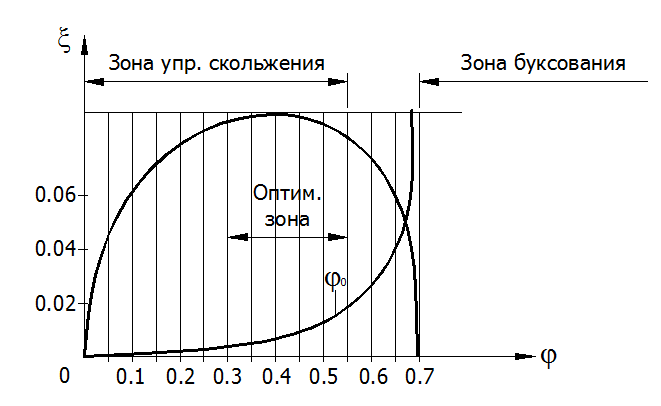
Рис.55

Залежність між коефіцієнтом тяги й коефіцієнтом пружного ковзання ременя, виражена графічно, зветься кривими: ковзання ременя. Ці криві для різних типів ременів будуються дослідним шляхом на установках, де ріст навантаження рівняється з відносним ковзанням ременя. До критичного значення j₀ залежність лінійна, що відповідає пружному ковзанню ременя; за критичною точкою починається нелінійна залежність, що відповідає буксуванню ременя. Оптимальний режим роботи ременя при вищому значенні ККД близький до критичної точки, але повинен перебувати в зоні пружного ковзання. На підставі кривих ковзання визначаються допустимі напряжения у ремені.

Напруги в ремені і їхня кругова епюра

1) напруга від окружного зусилля:

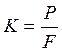
Для плоских ременів площа перерізу ременя

де b - ширина, d - товщина ременя.

Для клинових ременів F визначається по таблицях Дст.

2) напруга від попереднього натягу ременя:

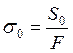
3) напруга від зусиль натягу ременя:

 

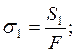
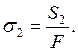
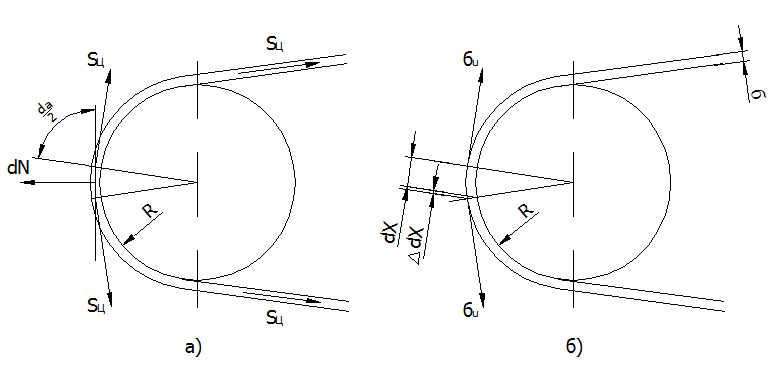
Рис. 56

4) напруга від дії відцентрових сил: Розглядаючи суму проекцій сил на горизонтальну вісь (мал.56 а), отримаємо:

Синус елементарного кута  можна прийняти рівним куту в радіанах ; тоді відцентрова сила елементарної ділянки ременя, введеного дугою :

                                           (1)

з іншого боку, елементарна відцентрова сила:

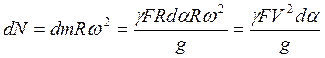     (2)

Тут: dm - елементарна маса виділеної ділянки ременя;

R -  радіус шківа;

w -  кутова швидкість обертання шківа;

g -  питома вага матеріалу ременя;

V -  окружна швидкість ременя;

g -  прискорення сили ваги.

Дорівнюючи рівняння (1) і (2) і зрівнюючи розмірності, отримаємо натяг ременя від дії відцентрової сили:

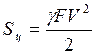
Напруга в ремені від дії відцентрової сили:

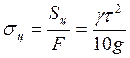
Варто помітити, що напруга пропорційно квадрату окружної швидкості; при малих швидкостях вона невелика, при великих - різко зростає.

5) напруга від вигину ременя:

Розглядаючи подобу фігур (мал. 56 б), можна написати:

; 

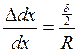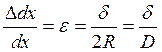
За законом Гука  ; 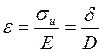, звідси

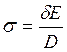
Напруга вигину пропорційно товщині ременя, модулю пружності й обернено пропорційна діаметру шківа. Це значить, що відношення  не повинне бути малим (воно вказується в таблицях ГОСТу для кожного типу ременя).

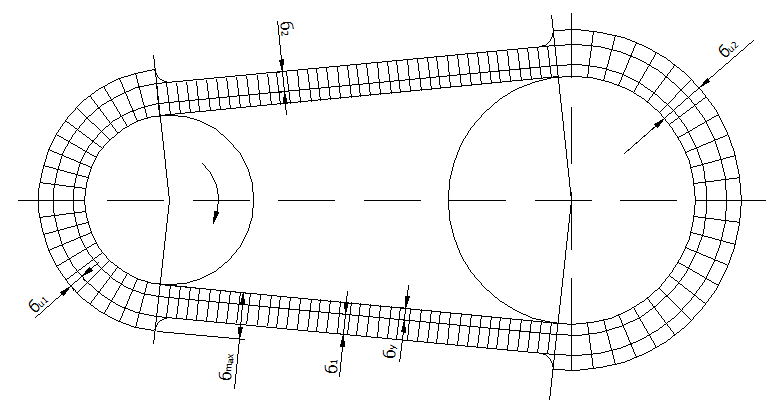
Рис. 57

Розрахунок пасових передач до тягової здатності

а) плоскі ремені:

; 

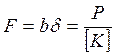Тут: [К] - розрахункова допустима напруга;

- табличне припуска напряжение, що;

C_H - поправочний коефіцієнт, що залежить від характеру навантаження;

C_V - поправочний коефіцієнт, що залежить від швидкості ременя;