Справочное руководство по физике для абитуриентов, поступающих в Российский государственный открытый технический университет путей сообщения, страница 7

 в)  при  решении  задач  на часы  с маятником нужно помнить, что   при  увеличении  длины   маятника  увеличивается  период  его колебания,  а   следовательно,  часы  отстают,  т.е.   их   “ход”  замед-ляется;

  г)  при   рассмотрении   волновых   процессов нужно учитывать,  что частота колебаний ν источника связана с длиной волны λ зависимостью

,

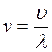где  скорость распространения волнового процесса в среде (электромагнитные волны распространяются в вакууме или воздухе со скоростью 3·10⁸ м/с).

          Общие замечания к решению задач на колебания и волны:

Если в задаче задано уравнение гармонических колебаний, то величины, характеризующие колебания (амплитуда, частота, фаза начальная фаза, период), могут быть найдены путем сопоставления данного уравнения с общим уравнением  гармонических  колебаний.

В задачах о математическом маятнике необходимо учитывать: если точка подвеса маятника движется ускоренно (или маятник приобретает ускорение при изменении силы натяжения нити), то период колебаний такого маятника изменяется. Ряд задач на электромагнитные колебания решаются с применением формулы Томсона и формулы емкости плоского конденсатора:

 и .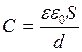

Пример№9

          Предмет находится на расстоянии 10 см от переднего фокуса линзы, а экран, на котором получается четкое изображение предмета, расположен за задним фокусом линзы на расстоянии 40см от него.  Найти  оптическую силу  линзы  и увеличение  предмета.

    Дано:

а =10см=0,1м                       А                               в

        в=40см=0,4м                                     _о                            В′

2F

                                              В а

        Д-?  Г-?                        2F           F                 F      2F              

                                                                                      А′

                                                      Рис.5

                        Решение:

          Согласно условию задачи изображение предмета (рис.5) действительное увеличение. Для решения задачи используем уравнение  тонкой  линзы.

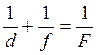
Исходя  из  рисунка  d = a + F; f = в + F

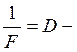оптическая  сила  линзы.

.

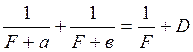D=, D=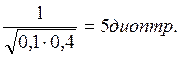

Увеличение  линзы:

F=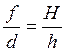, где  h = АВ; Н = А′ В′

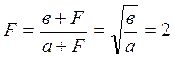
          Характерные ошибки: главные ошибки связаны с построением изображения и выбором знаков в уравнении тонкой линзы: 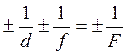. Знак  “+”  у  dи  f  берется при условии, если
d > F  и  f >F. Знак у F берется “+” для собирающей линзы и “-” у рассеивающей. По окончании решения часто требуется дать характеристику изображения предмета: действительное или мнимое, прямое или обратное (перевернутое), увеличенное или уменьшенное. 50% ошибок получается из за нечеткости построения точек и предметов в линзах.

          Общие замечания к решению задач на оптику: при решении задач данного раздел, важное значение имеет правильно сделанный чертеж. При решении часто используются геометрические и тригонометрические соотношения и преобра-зования.

При рассмотрении задач падения светового луча на границу раздела сред нужно внимательно определить углы падения, отражения и преломления, обратив внимание на соотношение величин показателей преломления сред n₁ и n₂ Нельзя путать два понятия: угол падения i и угол между падающим лучом и границей радиуса  сред α,  а  именно:

 

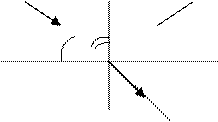                          i    i'

           n₁         α                          n₂>n₁

           n₂                     

          Основная масса задач на фотоэлектрический эффект решается с  применением  уравнения Эйнштейна  для  внешнего  фотоэффекта

hν= А_вых + Е_k ,

выражающего закон сохранения энергии. При условии Е_k = 0 (кинети-ческая энергия фотоэлектронов равна нулю) фотоэффект еще существует, а частота падающего света (ν = ν_кр) в этом случае называется красной границей фотоэффекта (минимальной  частотой,  обеспечивающей  фотоэффект).