Справочное руководство по физике для абитуриентов, поступающих в Российский государственный открытый технический университет путей сообщения, страница 4

   Разделив первое равенство на второе, получим

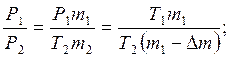
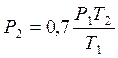
Проверка единиц измерения:

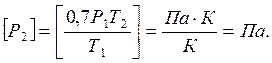
Расчет:

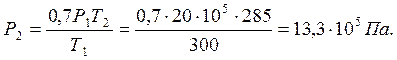
          Характерные ошибки: решение задач проводят с использо-ванием объединенного газового закона, забывая о том, что им можно пользоваться лишь в случае, когда масса газа в процессе нагревания (охлаждения), расширения (сжатия) остается неизменной. При изменении массы газа всегда нужно использовать уравнение Менделеева – Клапейрона. Другая часто встречающаяся ошибка – это кажущаяся нехватка данных для решения задач, хотя в условиях задач говорится о нормальных условиях, при которых находится газ. Введение сочетания “нормальные условия” говорит о том, что объем газа находится при давлении 1атм. = 1·10⁵ Па и температуре 0⁰С,  и  эти  данные можно использовать в решении. Наибольшее   количество   расчетных   ошибок   встречается   в   этом   разделе   за   счет   неумения   переводить   внесистемные единицы   измерения   давления и объема  в   систему   СИ:

1атм.  = 760 мм рт. ст. = 1,013·10⁵ Н/м² (Па);

1л =  1дм³  = 1· 10^-3  м ³.

          Общие замечания к решению задач раздела “Молекулярная физика и теплота”: если в задаче говорится о смеси   газов,   то   нужно   использовать   еще   закон   Дальтона

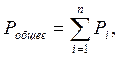 где Р- парциальное давление газов.

          Задачи об изменении внутренней энергии тел можно разделить на три группы. В задачах первой группы рассматриваются явления, где в процессе взаимодействия изменяется лишь их внутренняя энергия без совершения работы над внешней средой. Одни  тела, участвующие в теплообмене, при этом охлаждаются, другие – нагреваются. Основным расчетным уравнением для всех задач первой   группы   является   уравнение   теплового   баланса

.

В задачах второй группы рассматриваются явления, связанные с превращением одного вида энергии в другой при взаимодействии тел. Результат такого взаимодействия – изменение внутренней энергии одного тела вследствие совершенной им или над ним работы. Теплообмен между телами при этом, как правило, не учитывается. Основное расчетное  уравнение с учетом коэффициента   полезного   действия   η   имеет   вид

А = η ΔU.

          Задачи третьей группы объединяют в себе две предыдущие. При расчетах размерность молярной массы брать в системе
СИ: кг/моль.

Пример № 5

          Определить работу, совершаемую при перемещении точечного заряда q = 2·10⁶ Кл, из точки, находящейся на расстоянии r₁ = 20 см,  от заряда, создающего поле , до точки, расположенной на расстоянии r₂ = 50 см  от этого же заряда. Окружающая среда – воздух.

    Дано:                                                            Решение

q= 2·10^{- 4} Кл;            Работа, совершаемая при перемещении
r₁ = 20 см = 0,2 м;                заряда   в  электрическом поле,  .

Q = 1·10^-4 Кл;                          Потенциалы  поля,  которые создаются заря-

r₂ = 50 см = 0,5м;                 дом    на  расстояниях    и  ,  равны:

ε₀ = 8,85 ·10^-12 Ф/м;

ε = 1.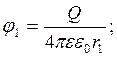                                                          

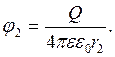
А - ?                          

Следовательно,

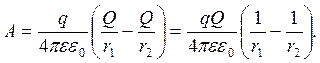
Проверка единиц измерения:

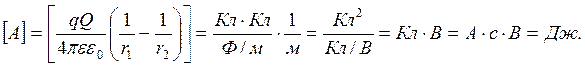
Расчет:

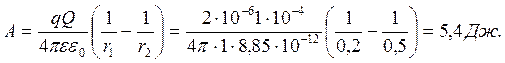
          Характерные ошибки: они заключаются в том, что абитуриенты не делают различия между зарядом, создающим поле, и пробным зарядом, с помощью которого исследуется поле. Так, например, уравнения для напряженности и потенциала поля можно выразить как через величину пробного заряда q,   так   и   через   величину   заряда,   создающего   поле  Q.

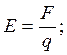
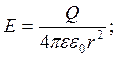
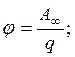
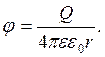
          Другая категория ошибок появляется при расчетах,  когда, решая задачу в системе СИ, не учитывают коэффициент 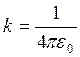, а отсюда   не   получается  и  проверка   размерности.