Рис. 1
![]() ср – ?
ср – ?
Решение
В задаче рассматривается равномерное движение одного тела. Делаем чертеж (рис. 1). Составляем уравнение перемещения для каждого отрезка пути:
S1 = ![]() 1t1;
S2 =
1t1;
S2 = ![]() 2t2; S3
=
2t2; S3
= ![]() 3t3
3t3
и записываем дополнительные условия
S1
= S2 + S3; t2 = t3; 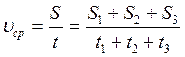
Имеем шесть уравнений и семь неизвестных
(S1, S2, S3, t1, t2, t3,
![]() ср), решаем систему относительно
искомой величины υср. Если при решении задачи полностью учтены все
условия, а в составленных уравнениях число неизвестных больше числа уравнений,
это означает, что при последующих вычислениях одно из неизвестных
сокращается, такой случай имеет место в данной задаче.
ср), решаем систему относительно
искомой величины υср. Если при решении задачи полностью учтены все
условия, а в составленных уравнениях число неизвестных больше числа уравнений,
это означает, что при последующих вычислениях одно из неизвестных
сокращается, такой случай имеет место в данной задаче.
Решение системы относительно средней скорости дает
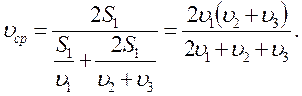
Проверка единиц измерения:
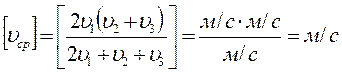
Расчет:
Подставляя числовые значения (с учетом их перевода в СИ) в расчетную формулу, получим:
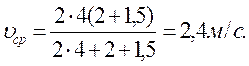
Характерные ошибки: часто при нахождении величины средней скорости ответ дают в виде
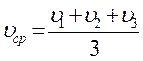 ,
,
т. е. находят среднюю скорость как среднее арифметическое заданных скоростей. Это неверно. Такое равенство может быть справедливо лишь при условии равенства времен движения на участках (t1 = t2 = t3).
Общие замечания к решению задач по кинематике: наибольшую трудность и большое количество ошибок дают задачи на движение одних тел относительно других, которые, в свою очередь, движутся относительно какой-то системы отсчета. Решение задач нужно начинать с выбора системы отсчета, установить подвижную и неподвижную системы отсчета, связав их с телами, относительно которых рассматривается движение. Составляя уравнения движения, необходимо следить за тем, чтобы начало отсчета времени было одинаковым для всех тел, участвующих в движении.
Решение задач о движении точки по окружности принципиально ничем не отличается от решения задач о прямолинейном движении. Особенность в том, что здесь наряду с общими формулами кинематики приходится учитывать связь между угловыми и линейными характеристиками движения.
Пример № 2
Два грузика с массами 5 кг и 3 кг соединены нерастяжимой нитью, перекинутой через неподвижный блок. Определить ускорение грузов, натяжение нити и давление на ось блока. Массой блока пренебречь.
 Дано:
Дано:

![]() g
= 9,8 м/с2;
g
= 9,8 м/с2;
m1 = 5 кг;
m2 = 3 кг;
![]()
![]()
![]() Т1
= Т2.
Т1
= Т2.
![]() ↓
↓![]() ↑
↑![]()
![]()
![]()
![]()
![]() Т
- ? а - ? F - ?
Т
- ? а - ? F - ?
![]()
![]() Решение
Решение
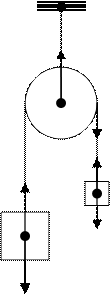
Груз m1 опускается вниз, а m2
![]() поднимается вверх
(рис. 2). Так
поднимается вверх
(рис. 2). Так
как массой блока
пренебрегаем, то
Рис.2 натяжение обеих частей нити долж-
ны быть одинаковы
Т1= Т2. Запишем
второй закон Ньютона для
каждого из
грузов:
m1a = m1g – T1; (1)
m2a = T2 – m2g. (2)
Решая совместно уравнения (1) и (2), получим:
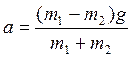 ;
; 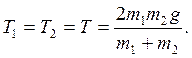
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.