Справочное руководство по физике для абитуриентов, поступающих в Российский государственный открытый технический университет путей сообщения, страница 3

Давление на ось блока F равно сумме натяжений нитей, т. е. F есть равнодействующая двух параллельных сил T′₁ и T′₂, для которых в свою очередь T₁ = T′₁ и T₂ = T′₂:

.

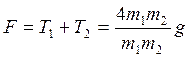Проверка единиц измерения:

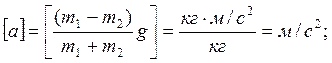
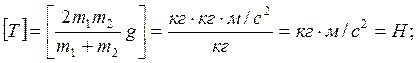
 [F] = [T] = H.

Расчет:

   

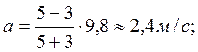
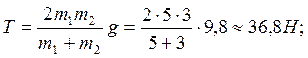
F = T₁ + T₂ = 2T = 73,6 H.

Характерные ошибки: основную долю ошибок дает неумение абитуриента расставить все силы, приложенные к материальной точке (телу, которое рассматривается изолированно от системы), движущейся в текущий момент времени, а также правильно указать силы, действующие на связи (нити, опоры, подставки), руководствуясь третьим законом Ньютона. Например, если на тело m₁ действует связь (нить) силой T₁, то и на нить действует сила
T′₁  = -T₁, и эти силы никогда не будут уравновешивать друг друга, так как приложены к разным телам. В противном случае будет происходить потеря сил и получится   неверное   решение.

Общие замечания к решению задач по динамике: при решении задач на соударение тел и составлении исходного уравнения особое внимание следует обращать на векторный характер величин, входящих во второй закон динамики, и учитывать знак при записи в скалярной форме. Если в задаче говорится о трении, то силу трения представляют через коэффициент трения k и силу нормального давления Р_н (силу, перпендикулярную поверхности движения):

                            F_тр = k·P_тр.

Пример № 3

Пуля массой m= 10г, летящая со скоростью  = 800 м/с, попадает в дерево и углубляется на 10 см. Найти силу сопротивления дерева и время  движения  пули  в нем, считая  движение    равнозамедленным.

Дано:                                                                   Решение

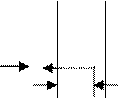
m = 10г = 1·10^-2 кг;                               Сделаем рисунок (рис.3)

=800м/с;         Применим второй закон Ньютона в
S = 10cм = 0,1м.                    формулировке,    что  изменение  импуль-

                                                са пули равно импульсу силы   сопро-
F- ?  t- ?                                тивления:

                                                   

 т                                                 ,

Рис.3

                                                       

Перейдем  от  векторной  формы  записи  к  скалярной.

В  проекции  на  ось х  и  с  учетом,  что    получим

отсюда

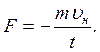
Время движения пули в дереве 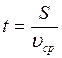. Так как  движение равнозамедленное, то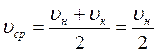         

Итак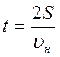  

        

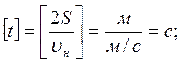
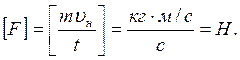
Расчет:

        

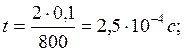
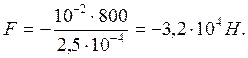
Характерные ошибки: при решении задач на движение, в том числе и для импульсов тел, нужно уравнения движения сначала записывать в векторной форме для замкнутой системы, а далее проектировать на выбранные оси координат. Четко определить вид удара: упругий или неупругий, помня, что при упругом ударе тела движутся   сами   по   себе,   а   при   неупругом,   как   единое  целое.

Для составления закона сохранения импульса необходимо выбрать систему отсчета, относительно которой данная система тел рассматривается.

Общие замечания: задачи данного типа могут решаться также  с  использованием  закона  сохранения  энергии:

Кинетическая энергия пули 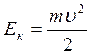 идет на работу против сил сопротивления  А = F ·S.

ΔE = A

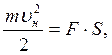 откуда  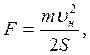так как

из предыдущего 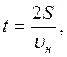 то получим

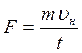
Пример № 4

Баллон содержит сжатый газ при 27⁰С и давлении
Р₁ = 20атм. Каково будет давление, если из баллона будет выпущено 0,3 массы газа,   а   температура   понизится   до 12⁰С ?

Дано:                                                                Решение

t₁⁰ = 27⁰C; T₁ = 300K;                 Рассмотрим два состояния газа: до разря – Р₁ = 20атм = 20·10⁵ Па;     жения и после него, когда осталось т₂ мас-                                     сы.Параметры каждого из этих состояний                                         Δт= 0,3т₁;         связаны уравнением Менделеева – Кла-                          t₂⁰ = 12⁰C;  T₂ = 285K.             пейрона

  Р₂ - ?                                                    

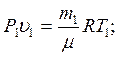
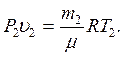
где μ - молярная масса газа;

      R  - универсальная газовая постоянная.