Справочное руководство по физике для абитуриентов, поступающих в Российский государственный открытый технический университет путей сообщения, страница 6

          На электрон, движущийся в магнитном поле, действует
 сила Лоренца (рис. 4). Направление силы Лоренца определяется правилом левой руки. Сила Лоренца перпендикулярна скорости  она не изменяет величину скорости, а лишь изменяет ее направление. Сила Лоренца в каждой точке траектории направлена к центру ее кривизны по радиусу R. Под действием этой силы электрон приобретает постоянное центростремительное ускорение, а это означает,  что  электрон  в магнитном поле движется по окружности.

          Силу Лоренца можно записать, используя:

второй закон Ньютона

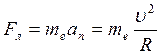                                                                                      (1)

или получить из закона Ампера

                                                                                           (2)

где 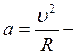 центростремительное ускорение;
       скорость электрона;
       α- угол между векторами  и , в нашем случае
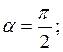
       m_e- масса электрона.

Решая совместно уравнения (1) и (2), получим

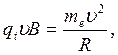
откуда

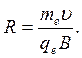
Проверка единиц измерения:

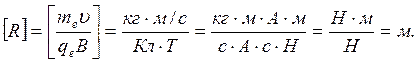
Расчет:

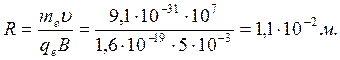
          Характерные ошибки: решения задач требуют записи применяемых законов и формул в общем виде с учетом углов между соответствующими векторами:

 

F_a = IBl  sin α,      где 

                                                                              

 sin α,    где  

 

                                    Ф = ВS cos α,        где 

 

 sin α,   где 

          При записи закона электромагнитной индукции надо помнить, что знак “минус” в формуле выражает правило Ленца и его необходимо учитывать при решении. Когда знак “минус” в конечной расчетной формуле уже не влияет на расчет требуемой величины, то ее надо взять по абсолютной величине.

          Общие замечания к решению задач по разделу “Магнитное поле. Электромагнитная индукция”: при решении задач, в которых рассматривается проводник или контур с током в магнитном поле, нужно на чертеже указать направление тока, направление вектора магнитной индукции и сил, действующих на проводник или контур.

          Задачи на движение заряженных частиц в магнитном и электрическом полях решаются в большинстве случаев путем составления уравнений движения материальной частицы с учетом всех действующих на нее сил.

Если требуется найти ЭДС индукции, то сначала необходимо установить, изменением какой величины  (Sили  α) вызывается изменение потока магнитной индукции ΔФ а затем воспользоваться законом электромагнитной индукции.

Пример№8

          Маленький шарик подвешен на нити длиной 1,5 м к потолку вагона. При какой скорости вагона шарик будет особенно сильно колебаться под действием ударов колес о стыки рельсов? Длина рельса 18,0 м.

Дано:                                              Решение:

t = 1,5м;               Необходимо отметить, что мы имеем

L = 18м.          математический  маятник,  который  совершает  вынуж-

                      денные колебания с частотой ν,  равной частоте  ударов

              колес  о  стыки  рельсов

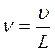                                                  ,                                                    (1)

где  - скорость равномерного движения вагона.

          Так как по условию задачи шарик при этом имеет максимальное  отклонение,  то  воспользуемся  условием  резонанса:

,

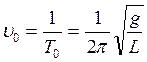                                 где    ;                                         (2)

-частота собственных колебаний шарика.

Решая   совместно   уравнения  (1)  и  (2),   получим:

   ;       .

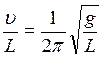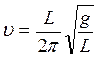Проверка единиц измерения:

.

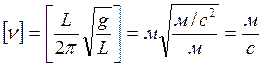Расчет:

                                 .

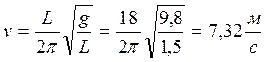          Характерные ошибки: ввиду того, что данный раздел охватывает большой объем теоретического материала, выделим   несколько   видов   ошибок:

          а)  при  преобразовании  уравнения   смещения   (скорости, , заряда)   при   гармонических   колебаниях

;

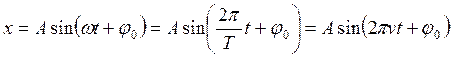 б)  при  расчетах  в  системе СИ  фаза колебания (и начальная фаза)  измеряется  в  радианах,  частота ν  и  циклическая  частота  колебаний   ω  измеряются  в Гц = 1/с;