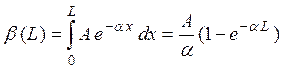 .
.
Далее, примем, что объект рассматривается на фоне, в качестве которого выступает небо у горизонта. Яркость такого «фона» - β(∞)=А/α. Предположим также, что объект имеет нулевую собственную яркость (черный щит). Тогда его видимая яркость, обусловлена исключительно рассеянием излучения в воздухе, заключенном в выделенном объеме, а контраст, образуемый яркостями объекта и фона, будет равен
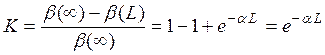 .
.
Полагая К=ε=0.02, находим для метеорологической дальности видимости
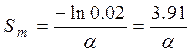 .
.
Под метеорологической дальностью видимости понимается наименьшее расстояние, с которого в светлое время суток теряется видимость абсолютно черного объекта, проецирующегося на фоне безоблачного неба у горизонта и имеющего угловые размеры не меньше 20 угловых минут (1/50 расстояния до наблюдателя).
Определив Sm, мы можем получить хорошую оценку для α и использовать ее для расчета любых других дальностей видимости.
В настоящее время для определения дальности видимости используется измерение коэффициента ослабления α воздуха по результатам регистрации излучения лампы или мощного светодиода на достаточно длинной трассе. Согласно приведенной выше формуле
![]() ,
,
то есть, оптическая толщина слоя атмосферы на пути длиной, равной дальности видимости, приблизительно равна 4. Отсюда следует, что при дальности видимости в пределах 10-20 км, коэффициент ослабления α составляет 0.4-0.2 км-1. При этом оптическая толщина трассы длиной около 100 м будет составлять 0.04-0.02. Для обеспечения менее чем 10%-й ошибки определения дальности видимости, ошибка измерений оптической толщины трассы не должна превышать 0.004-0.002. Это вполне осуществимое требование.
[1] Поглощение забирает энергию излучения и превращает ее в другие виды энергии (в первую очередь, в тепловую, хотя поглощенная энергия может также трансформироваться в энергию излучения на других длинах волн, а сам процесс перехода поглощенной энергии в тепловую может быть разделен на несколько промежуточных этапов. Под рассеянием понимается процесс, когда часть энергии падающего излучения испускается (переизлучается) элементарным объемом в других направлениях. Во всех случаях в данной книге, если специально не оговорено, подразумевается, что рассеяние не меняет частоты или энергии фотона. Эффективность рассеяния зависит от угла между направлением рассеянного излучения и направлением падающего излучения. Эта зависимость описывается так называемой индикатрисой рассеяния.
[2] Помимо условия линейности процесса взаимодействия излучения со средой (пропорциональности доли поглощенной тонким слоем энергии излучения энергии падающего излучения) для выполнения закона Бугера требуется, чтобы излучение было монохроматичным (то есть, относилось к бесконечно узкому интервалу длин волн). Это важно для случаев, когда оптическая толщина зависит от длины волны.
[3] Конечно же, здесь речь идет о спектральной плотности мощности, отнесенной к единичному интервалу длин волн.
[4] Действуя по аналогии, легко получить выражение для яркости атмосферы, наблюдаемой из космоса (сверху).
[5] Хотя точно сосчитать эти значения уже не так просто.
[6] Похожий вариант метода используется для определения общего содержания озона и его вертикального распределения по результатам измерения спектральной яркости атмосферы в ультрафиолетовой области спектра с помощью аппаратуры, устанавливаемой на борту космических аппаратов. В настоящее время это единственный метод позволяющий получать ежедневные глобальные карты общего содержания озона. Точность методики, правда, не очень высока, и для ее повышения используется привязка полученных результатов к данным наземных измерений в нескольких контрольных точках земного шара.
[7] Конечно же, величина рассеиваемой энергии излучения меняется в зависимости от условий освещения и метеоусловий. Однако для нас сейчас важно только то, что эта величина одинакова для всех элементарных объемов внутри рассматриваемого телесного угла.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.