Характеристики поля излучения и уравнение переноса излучения, страница 2

Выражение для плотности потока можно переписать ещё так: Н =Н⁺-Н ^- где,

                                   .

Здесь проведено разделение на потоки, падающие на площадку из верхней и нижней полусфер (если площадка ориентирована горизонтально). Если I не зависит от направления, тогда такие потоки равны,  и суммарная плотность потока равна нулю. Плотность потока из верхней полусферы H⁺ еще называют освещенностью (количество энергии излучения, падающего из верхней полусферы на горизонтальную площадку единичной площади в единицу времени).

6.1. Уравнение переноса излучения

При распространении в среде на пути dk (по направлению k) энергия излучения  может измениться за счёт процессов ослабления и испускания.

                                              dE= - dE^осл+ dE^исп.

Считая, что ослабление линейно зависит от интенсивности и массы вещества (закон Бугера) имеем

                          dE^осл=αdkIdSdΩdt.                                                                        

где αdk – доля излучения, ослабленного на пути dk. Коэффициент α называется показателем или коэффициентом полного ослабления.  В общем случае

                                                                    α = æ + σ,

где æ – коэффициент истинного поглощения, σ - коэффициент  рассеяния. Это единственные два процесса, которые могут приводить к отбору энергии излучения, приходящего в объем[1]. Из выражения для dE^осл следует, что αdk - безразмерный множитель. Следовательно, размерность [α]=см^-1.

Излучение может испускаться рассматриваемым объемом за счет рассеяния, а также за счет процессов, не связанных с проникающим в объем внешним излучением (в частности, это может быть тепловое излучение среды). Обозначим количество энергии, испускаемое единичным объёмом среды в единичном телесном угле за единицу времени, J (коэффициент испускания). Тогда

                                 dE^исп=JdVdΩdt ,  dV=dSdk.

Мы здесь не конкретизируем причину, вызывающую испускание излучения, а просто предполагаем, что нам в каждой точке пространства и в каждый момент времени известен коэффициент испускания. В случае необходимости можно ввести зависимость коэффициента испускания от всевозможных физических характеристик (например, от направления распространения излучения).

С учетом сказанного  имеем

                   dIdSdΩdt=dE =-αdkIdsdΩdt+JdkdsdΩdt,

откуда следует уравнение переноса излучения:

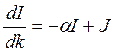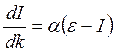                         или           .                                               (6.1)

Здесь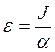 называется функцией источников.

Уравнение переноса излучения  является математической формулировкой закона сохранения лучистой энергии при взаимодействии излучения с элементарным объёмом вещества. Введём оптическую толщину dτ = αdk. Тогда

                              .

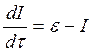Приведенное соотношение называется уравнением Шварцшильда (Karl Schwarzschild, 1873-1916, известный немецкий физик и астроном).

В общем случае уравнение переноса является интегро-дифференциальным (функция источников ε может быть интегралом от I). Кроме того,

               ,  

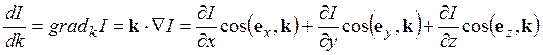где  - единичные орты осей . Угол между направлением kи ортом оси x обозначен как (e_x,k). Решение уравнения переноса осложняется также наличием  зависимости æ и σ от частоты. Все это настолько усложняет проблему, что аналитические решения уравнения переноса излучения получены только для нескольких простейших случаев.

Пусть I(0)  - интенсивность излучения, падающего перпендикулярно на границу среды (k=0), и пусть 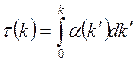- оптическая толщина среды на пути от границы до точки k. Если имеется только поглощение (нет источников излучения в среде), то 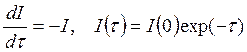 , и мы получаем закон Бугера[2].

Функция источников ε является важнейшей характеристикой взаимодействия излучения с веществом. Возникновение излучения в некотором объёме происходит либо вследствие испускания собственного излучения объёмом, либо действия падающего излучения (например, рассеяния излучения). Часто при решении задач переноса  теплового излучения используют так называемое условие локального термодинамического равновесия.    Это означает, что каждый элементарный объём рассматривается, как находящийся в термодинамическом равновесии при некоторой температуре Т. Этой температурой определяется функция источников – излучение абсолютно чёрного тела. Такое приближение допустимо, когда можно пренебречь отсутствием равновесия излучения со средой. В подобной  ситуации температура падающего излучения не совпадает с температурой среды, а температура испускаемого излучения соответствует температуре среды: