Характеристики поля излучения и уравнение переноса излучения, страница 3

                                 Т ^{падающего излучения} ≠  Т ^среды =  Т ^{испуск.излуч}.

6.2. Рассеяние света

Излучение в среде может испытывать истинное поглощение, характеризуемое коэффициентом поглощения  æ. Остальная часть задерживаемого средой излучения вновь испускается. Один из механизмов испускания поглощенного излучения – рассеяние. Коэффициенты ослабления и рассеяния  среды, состоящей из невзаимодействующих элементов,  рассчитываются по теории Ми (Gustav Mie, 1908), в основе которой – задача о рассеянии плоской электромагнитной волны однородным диэлектрическим шаром.

Величина 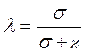,  (α = æ +σ) называется вероятностью выживания кванта. Она показывает долю рассеянных фотонов из всех, задержанных в единичном  объёме. Значению λ=1  соответствует только рассеяние без поглощения излучения.

Рассеянное излучение анизотропно,  то есть, эффективность рассеяния зависит от направления. Для учёта этого обстоятельства в случае изотропной среды вводят вероятность рассеяния под углом γ внутри телесного угла dΩ: i(γ)dΩ, когда рассеяние определенно произошло. Угол γ   между первоначальным направлением распространения излучения и направлением рассеянного излучения  называют углом рассеяния. Функцию i(γ)  называют индикатрисой рассеяния. Очевидно, должно выполняться условие

                                                  ,                                                          

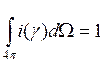которое означает, что вероятность рассеяния под каким-нибудь углом равна 1. Если 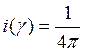= constимеем случай изотропного рассеяния, а индикатриса называется сферической. Согласно определению, индикатриса рассеяния определяет вероятность рассеяния в единичный телесный угол по заданному направлению, если сам факт рассеяния определенно произошел. Полная вероятность рассеяния фотона, задержанного в единичном объеме среды, в заданном направлении, очевидно, есть произведение вероятности выживания кванта на соответствующее значение индикатрисы.

Если рассеяние происходит на частицах, размеры которых малы по сравнению с длиной волны излучения, индикатриса рассеяния имеет вид 

                                               ,                                                             

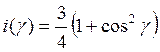а рассеяние называется рэлеевским (John William Rayleigh). С увеличением размера частиц индикатриса  становится всё более вытянутой вперёд, а зависимость коэффициента рассеяния от длины волны излучения становится всё более сложной. Еще более сложные ситуации возникают в случае, когда форма частиц отличается от сферической, и в воздухе присутствуют частицы разных размеров.

Если известны α, λ, i(γ),  можно подсчитать, сколько излучает выделенный объём в заданном направлении:

                                                λi(γ)dE^осл  – 

доля энергии падающего излучения, задержанного объёмом и затем испущенного в результате процессов рассеяния. Здесь λ – вероятность выживания кванта, а не длина волны. С учётом всех направлений приходящего излучения для коэффициента испускания и функции источников имеем

                                       ,                          

              ,

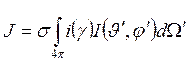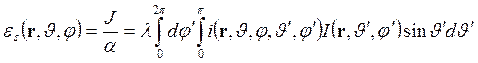где угол рассеяния определяется направлениями распространения падающего и рассеянного излучений, и во второй формуле выражается через углы сферической системы координат, определяющие названные направления:  соответственно. В последней формуле радиус-вектор r, фиксирует положение точки среды, а углы  - направление распространения испускаемого излучения. Сюда надо ещё добавить граничные условия, описывающие характеристики падающего излучения на границе среды, чтобы полностью определить задачу переноса излучения.

6.3. Методы решения уравнения переноса излучения

Уже говорилось, что строгое решение уравнения переноса излучения возможно только в нескольких простейших случаях. Для получения  решений  практически важных задач развиты приближенные методы. Разработаны и вполне доступны всевозможные компьютерные программы, реализующие различные приближенные методы решения уравнения переноса излучения. Целая совокупность методов использует разложение в ряды по известным функциям, аппроксимирующим угловые характеристики излучения достаточно малым числом членов разложения.