Одним из наиболее оригинальных методов является метод Монте-Карло или метод статистических испытаний. Метод непосредственно использует представление об излучении как потоке частиц – фотонов и прослеживает судьбу каждого из испущенных источником фотонов, моделируя его траекторию. Метод является статистическим по природе и использует генератор случайных чисел для моделирования направления и расстояния, которое пролетает отдельный фотон до акта поглощения или рассеяния. В первом случае история «жизни» фотона заканчивается, во втором – случайным образом (с учетом индикатрисы рассеяния) выбирается направление рассеяния, и повторяются шаги, описанные выше. «Выпустив» достаточно большое число фотонов из источника и следуя приведенной схеме, можно найти, сколько испущенных фотонов попадает в данную точку пространства и по какому направлению. Это позволяет получить приближенные оценки характеристик поля излучения в заданной точке. Понятно, что для получения приемлемой точности число испущенных фотонов должно быть значительным.
Метод последовательных приближений формально сводится к представлению искомой интенсивности в виде ряда
![]() ,
,
где λ – вероятность выживания фотона. Конечно же, все величины в этой формуле в общем случае являются функцией координат. Значению k=0 соответствует вклад в интенсивность прямого излучения, достигающего данной точки пространства; k=1 – вклад в интенсивность за счет излучения, претерпевшего однократное рассеяние в среде на пути к рассматриваемой точке. Аналогично, I2 – вклад дважды рассеянного излучения и т.д.
Вообще говоря, существует весьма
серьезная проблема сходимости такого разложения. Кроме того, чем выше порядок
рассеяния, тем сложнее подсчитать соответствующий вклад. Что касается задач
атмосферной оптики, то Дейвом (Dave) было показано, что начиная с
определенного значения k (порядка рассеяния), члены Ik становятся близки к геометрической
последовательности. Тогда остаток ряда очень легко посчитать, зная отношение ![]() . Кроме того, при сильном поглощении средой
(малых величинах λ) разложение сходится достаточно быстро. В частности,
в области ультрафиолетового спектра для длин волн короче 300 нм вклад двукратного
и рассеяния более высоких порядков составляет не более нескольких процентов.
Это позволяет в ряде случаев ограничиваться учетом только однократно
рассеянного излучения.
. Кроме того, при сильном поглощении средой
(малых величинах λ) разложение сходится достаточно быстро. В частности,
в области ультрафиолетового спектра для длин волн короче 300 нм вклад двукратного
и рассеяния более высоких порядков составляет не более нескольких процентов.
Это позволяет в ряде случаев ограничиваться учетом только однократно
рассеянного излучения.
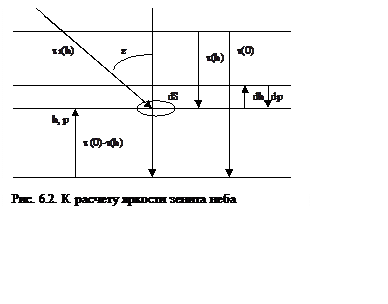 В качестве простого примера давайте посмотрим, как
определить яркость зенита неба в приближении однократного рассеяния при
отсутствии поглощения и аэрозолей (только молекулярное рассеяние). Здесь мы
предполагаем, что атмосфера плоская. Такое предположение вполне приемлемо в большинстве
практически важных случаев, когда зенитный угол Солнца не превышает 50 – 60
градусов.
В качестве простого примера давайте посмотрим, как
определить яркость зенита неба в приближении однократного рассеяния при
отсутствии поглощения и аэрозолей (только молекулярное рассеяние). Здесь мы
предполагаем, что атмосфера плоская. Такое предположение вполне приемлемо в большинстве
практически важных случаев, когда зенитный угол Солнца не превышает 50 – 60
градусов.
Пусть на верхнюю границу атмосферы
(см. рис. 6.2) падает параллельный пучок излучения со спектральной плотностью
потока ![]() (энергия излучения в единичном интервале
длин волн, падающая за единицу времени на единичной площади площадку, ориентированную
перпендикулярно направлению распространения излучения). На пути до уровня hатмосферы прямое излучение ослабляется
в 1/
(энергия излучения в единичном интервале
длин волн, падающая за единицу времени на единичной площади площадку, ориентированную
перпендикулярно направлению распространения излучения). На пути до уровня hатмосферы прямое излучение ослабляется
в 1/![]() раз, где, согласно приведенной на рис. 6.2
схеме,
раз, где, согласно приведенной на рис. 6.2
схеме, ![]() , а
, а ![]() -
оптическая толщина атмосферы от ее верхней границы до уровня h в
вертикальном направлении. Аналогично, путь излучения через тонкий слой толщиной
dh (dp в единицах давления) равен
-
оптическая толщина атмосферы от ее верхней границы до уровня h в
вертикальном направлении. Аналогично, путь излучения через тонкий слой толщиной
dh (dp в единицах давления) равен
![]() ,
,
где
z - зенитный угол Солнца (угол падения
солнечного излучения на плоскую атмосферу). На этом пути доля рассеиваемой по
всем направлениям энергии равна ![]() , а доля энергии,
рассеиваемой в единичный телесный угол вертикально вниз равна
, а доля энергии,
рассеиваемой в единичный телесный угол вертикально вниз равна ![]() . Здесь i(z) – значение индикатрисы
рэлеевского рассеяния для угла рассеяния z, σ – коэффициент рассеяния.
. Здесь i(z) – значение индикатрисы
рэлеевского рассеяния для угла рассеяния z, σ – коэффициент рассеяния.
Таким образом, элемент объема
атмосферы dV=![]() на высоте hрассеивает в единичный телесный угол в
направлении линии наблюдения мощность[3]
на высоте hрассеивает в единичный телесный угол в
направлении линии наблюдения мощность[3]
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.