На самом деле, озоновый слой нельзя считать тонким: концентрация озона непрерывно меняется с высотой от поверхности Земли до высот порядка 50 км, проходя через максимум на высотах от 15 до 25 км. Однако оказывается, что яркость зенита ясного неба в ультрафиолетовой области спектра зависит от формы кривой вертикального распределения концентрации озона подобно тому, как в случае с тонким поглощающим слоем. Понятно, что в данном случае нужно определить значительно больше неизвестных величин по сравнению с двумя в рассмотренном выше примере. От этого задача становится чрезвычайно сложной, но в принципе может быть решена, если проведено достаточно много измерений[6]. Помимо метода обращения для получения информации о вертикальном распределении озона с помощью наземной аппаратуры используются лидарная и микроволновая методики, а также аппаратура, устанавливаемая на шарах-зондах.
Метеорологическая дальность видимости Sm - это одна из величин, мониторинг которой ведется на всех метеорологических станциях мира. Как мы выясним, она непосредственно связана с коэффициентом ослабления видимого излучения в приземном слое воздуха.
Замечание: Кроме метеорологической дальности видимости существуют и другие «дальности»: обнаружения, потери видимости, узнавания и т.д.
Прежде всего обсудим абсолютно необходимый вопрос о контрастной чувствительности глаза. Мы можем видеть некоторый объект достаточных угловых размеров лишь в случае, если он отличается по яркости или цвету от фона, окружающего его. Это различие характеризуется так называемым контрастом (яркостным или цветовым). Обычно при рассматривании удаленных объектов решающее значение имеет именно яркостный контраст:
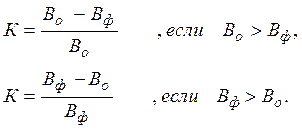
Предельными значениями контраста являются К=0, если Во=Вф (яркости объекта и фона совпадают), и К=1, если меньшая яркость равна нулю (то есть, предмет или фон можно рассматривать как абсолютно черное тело при температуре Т=0оК). При К=0 и одинаковом цвете объекта и фона мы его просто не увидим, какова бы ни была его яркость.
На самом деле человеческий глаз перестает чувствовать разницу при К>0. Наименьшее значение контраста, при котором глаз перестает его воспринимать, называется порогом контрастной чувствительности глаза и обозначается символом ε. Таким образом, уменьшение контраста до К= ε означает переход к невидимости предмета.
Величина ε несколько различается для разных наблюдателей и сильно зависит от условий наблюдения, прежде всего, от величины освещенности. При нормальном дневном освещении и достаточных угловых размерах объекта полагают ε=0.02. В сумерки и ночью порог возрастает до 0.6-0.7.
Вернемся теперь к проблеме определения метеорологической дальности видимости. Рассмотрим некоторый экран Р, видимый из точки О на расстоянии L внутри телесного угла dω(см. рис. 6.3). Если яркость экрана равна В, то световой поток от него дойдет до глаза ослабленным в 1/е–αL раз, где α - коэффициент ослабления (усредненный по спектру) в видимой области спектра. Поэтому яркость экрана, воспринимаемая глазом, будет равна
.
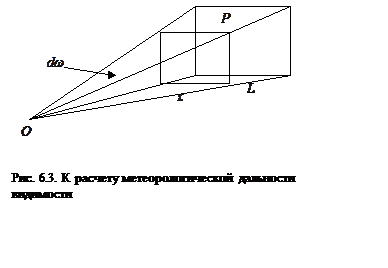Однако и воздух, заключенный между глазом и экраном,
будет также давать свой вклад в наблюдаемую яркость за счет рассеяния
солнечного излучения. Мы примем, что во всем объеме, заключенном в dω от точки наблюдения
до экрана, условия освещения солнечным прямым, рассеянным и отраженным от
поверхности Земли и облаков излучением одинаковы. Это будет означать, что
величина рассеиваемой элементарным объемом энергии излучения не зависит от
положения этого объема[7].
На расстоянии х элемент объема dV=x2dωdx имеет яркость dβ=Adx (величина Aзависит от освещенности и коэффициента рассеяния, но, как мы предположили, одинакова в пределах всего объема воздуха, заключенного между глазом наблюдателя и экраном). Поэтому яркость тонкого слоя воздуха толщиной dxв точке О воспринимается как е-αxAdx. Чтобы получить суммарную добавку к видимой яркости объекта за счет рассеяния солнечного излучения внутри телесного угла dω нужно проинтегрировать по х:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.