Характеристики поля излучения и уравнение переноса излучения, страница 5

Здесь в качестве множителя введен для учета того, что излучение падает не перпендикулярно на рассматриваемую площадку. Если теперь разделить результат на dS, получим вклад в спектральную яркость зенита неба за счет слоя dh при наблюдении снизу[4]. Нужно только учесть, что на пути к поверхности Земли это излучение будет ослаблено в 1/ раз. Поэтому

                                ,

а полная наблюдаемая спектральная яркость зенита неба в приближении однократного рассеяния равна 

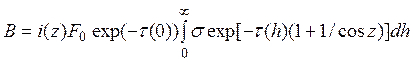                          .                                    Здесь индикатриса рассеяния вынесена из-под знака интеграла, поскольку угол рассеяния не зависит от высоты, и индикатриса молекулярного рассеяния не зависит от высоты. Напротив, объемный коэффициент рассеяния существенно зависит от высоты и не может быть вынесен из-под знака интеграла. 

Приведенное выражение  удается проинтегрировать в случае, когда имеем дело с чисто рассеивающей рэлеевской атмосферой (нет поглощения и рассеяния на аэрозолях). Тогда оптическая толщина формируется исключительно за счет рэлеевского рассеяния, и с высокой точностью справедлива эмпирическая формула  [34]

                                               .

Здесь  - оптическая толщина рассеяния вертикальным столбом атмосферы над уровнем h, β – эмпирический коэффициент, зависящий от длины волны излучения, p - давление воздуха на высоте h. Согласно приведенной выше формуле,

                                               ,

где знак минус введен, чтобы учесть противоположность знаков величин dp и dh. С другой стороны, согласно определению коэффициента рассеяния,

                                                .

Сравнивая два выражения, для объемного коэффициента рэлеевского рассеяния находим

                                              ,

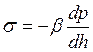то есть, коэффициент рассеяния пропорционален вертикальному градиенту давления. Подставляя найденное соотношение в выражение для яркости и проводя замену переменных, получаем

                        .

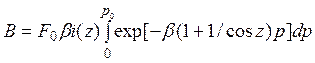Здесь p₀ – давление у поверхности Земли.Этот интеграл уже легко берется, поскольку множитель у давления в экспоненте постоянен. 

Влияние на яркость зенита неба поглощающего слоя. Метод обращения

  Теперь давайте посмотрим, как будет меняться яркость зенита неба в зависимости от высоты положения в атмосфере тонкого поглощающего слоя. Пусть оптическая толщина поглощения слоя в вертикальном направлении равна τ_п, а яркость зенита неба в отсутствие слоя – B. Предположим сначала, что поглощающий слой находится у поверхности Земли. Очевидно, что в этом случае рассеянное атмосферой излучение, распространяющееся вертикально вниз на последнем этапе ослабляется в 1/ раз. Поэтому для наблюдаемой яркости получим

                                                        .

Здесь 0 в аргументе функции Bозначает высоту поглощающего слоя.

Если поглощающий слой находится на верхней границе атмосферы, мы можем интерпретировать его наличие, как ослабление падающего на атмосферу солнечного излучения. В этом случае следует только учесть, что солнечное излучение падает на атмосферу  (и, соответственно, на поглощающий слой) под углом z. Поэтому оно ослабится в  1/ раз. Очевидно, во столько же раз ослабится наблюдаемая яркость, поскольку она пропорциональна интенсивности падающего излучения (это абсолютно верное утверждение в линейной теории переноса излучения). Следовательно, для наблюдаемой яркости получим

                                            .

Таким образом, в случае, когда Солнце не находится в зените, наблюдаемая яркость зенита неба зависит от высоты расположения поглощающего слоя (очевидно, что в интервале высот  яркость будет принимать некие промежуточные значения между двумя крайними случаями[5]).

  Рассмотренный выше пример является иллюстрацией идеи измерения вертикального распределения концентрации озона в атмосфере так называемым методом обращения. В ультрафиолетовой области спектра 290 – 330 нм озон является чуть ли не единственным поглотителем солнечного излучения (по крайней мере, самым сильным поглотителем). Если бы озоновый слой был достаточно тонким, регистрируя яркость зенита неба при  разных зенитных углах Солнца, или на  разных длинах волн, или при разных углах и на разных длинах волн вместе, можно было бы легко определить оптическую толщину озонового слоя (то есть, общее содержание озона в атмосфере) и высоту его расположения.