Явления переноса в газах: Учебно-методическое обеспечение практического занятия

6.5. Явления переноса в газах

 (4 часа)

6.5.1. Учебная цель занятия

Научить студентов применять следующие понятия и законы: длина свободного пробега молекул, среднее число соударений в единицу времени, эффективный диаметр и эффективное сечение молекул. Показать, что перенос массы вещества, передача импульса и теплоты объединяются общим понятием: явления переноса, поскольку механизм данных процессов – хаотическое тепловое движение атомов и молекул.

6.5.2. Методические указания к проведению
занятия

         Задачи данного раздела посвящены применению эмпирических законов переноса в газообразных средах, как наиболее простых. В жидких и твёрдых телах процессы переноса значительно сложнее по своему механизму, поэтому в данном разделе не рассматриваются,

Анализ задач начинается с определения эффективных значений параметров молекул: эффективного диаметра и сечения, а также средних значений скоростей их хаотического теплового движения. Для лучшего понимания рассматриваемых явлений важно привлекать молекулярно-кинетические представления. Обратить особое внимание на взаимосвязь коэффициентов переноса и их зависимость от давления и температуры.   Показать, что состояние вакуума обусловлено не давлением в сосуде, а в первую очередь длиной свободного пробега молекулы.

6.5.3. Рекомендуемая литература

[2] 3.6; 4.1-4.4;  [6] стр. 267-270.

6.5.4. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

Пример 1. Найти число всех столкновений Z, которые происходят в течение секунды между всеми молекулами водорода , находящимися в сосуде емкостью 20,0 л при температуре 300 К и давлении 101 кПа. Газ считать идеальным.

Если умножить число столкновений , испытываемых одной молекулой за 1 с, на число  (где  – число всех молекул, а единицу вычитаем, так как молекула сама с собой не сталкивается), то получится результат, превышающий в два раза искомое число . Действительно, в одном столкновении участвуют сразу две молекулы, поэтому в число  каждое столкновение входит дважды: один раз в счет столкновений первой молекулы данной пары, другой раз – в счет столкновений второй молекулы той же пары. Следовательно, правильным будет следующее выражение:

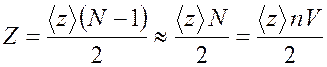.                       (16.2)

Подставив формулу (16.1) в выражение (16.2), получим

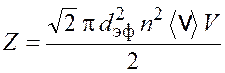.                               (16.3)

Концентрацию молекул найдем по формуле

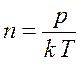,                                           (16.4)

где  – постоянная Больцмана.

Средняя скорость молекул

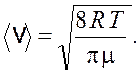                                       (16.5)

Подставив формулы (16.4) и (16.5) в выражение (16.3), получим

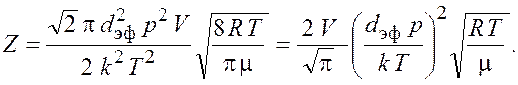
Подставим числовые значения и получим

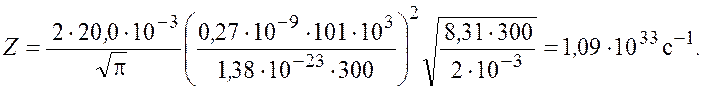
Ответ:

       Пример 2. Находящийся между стенками дюаровского сосуда воздух при температуре 20 °С оказывает давление 333 мкПа. Найти давление на стенки сосуда, если в него налить жидкий азот при температуре 78 К. Температура наружных стенок неизменна. Расстояние между стенками равно 1 см.

где  – эффективный диаметр молекул;  – концентрация молекул; k – постоянная Больцмана; T – термодинамическая температура; p – давление.

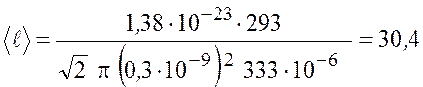Эффективный диаметр молекул воздуха примем равным  м. Подставим числовые значения и получим

 м.

Таким образом, . Следовательно, соударениями молекул друг с другом можно пренебречь и учитывать только удары молекул о стенки сосуда.

Можно предположить, что в пространстве между стенками дюаровского сосуда имеются как бы два встречных потока молекул. Один поток состоит из молекул, летящих от более нагретой стенки со среднеквадратичной скоростью  и имеющих среднюю энергию, соответствующую температуре . Другой поток состоит из молекул, летящих от холодной стенки со среднеквадратичной скоростью  и имеющих среднюю энергию, соответствующую температуре . Среднеквадратичные скорости молекул рассчитываются по следующим формулам:

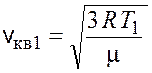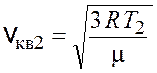,          .                    (17.2)

Молекулы газа подлетают к стенке с одной скоростью, а после взаимодействия со стенкой отлетают с другой скоростью, соответствующей температуре стенки. Механизм изменения скорости выглядит следующим образом. На поверхности каждой стенки существует слой адсорбированных молекул газа (в нашем случае кислорода и азота). Температура слоя равна температуре стенок. Этот слой молекул находится в динамическом равновесии с молекулами газа: молекулы из объема газа подлетают к стенке и “прилипают” к ней; одновременно из слоя вылетают, “испаряются” молекулы (происходит реадсорбция молекул) со средней кинетической энергией, соответствующей температуре стенки. Импульс силы, который получает стенка в результате этих двух процессов, такой же, как при отражении молекул от стенки, а не как при поглощении. Подлетающую и отлетающую молекулы можно рассматривать как одну молекулу, претерпевшую частично упругий удар о стенку.