|
Дано: |
Решение |
|
|
Найдем среднюю длину свободного пробега молекул воздуха, заключенного между стенками дюаровского сосуда,
где |
Эффективный диаметр молекул воздуха ![]() м.
Подставим числовые значения для первого случая и получим
м.
Подставим числовые значения для первого случая и получим
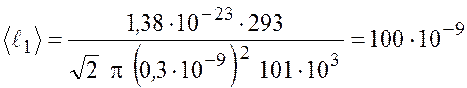 м.
м.
Подставим числовые значения для второго случая и получим
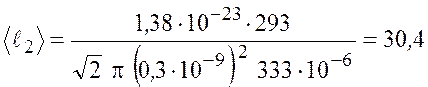 м.
м.
В первом случае ![]() .
Следовательно, можно использовать закон Фурье
.
Следовательно, можно использовать закон Фурье
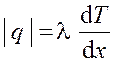 , (20.2)
, (20.2)
где ![]() – плотность теплового
потока;
– плотность теплового
потока; ![]() – коэффициент теплопроводности.
– коэффициент теплопроводности.
Предположим, что температура между стенками линейно меняется
с расстоянием. Тогда проекция градиента температуры на ось ![]() найдем по следующей формуле:
найдем по следующей формуле:
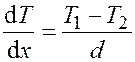 .
.
Количество теплоты, получаемой холодной стенкой,
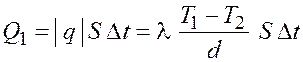 , (20.3)
, (20.3)
где ![]() – площадь поверхности
стенок сосуда;
– площадь поверхности
стенок сосуда; ![]() – время.
– время.
Считая воздух идеальным газом, коэффициент теплопроводности можно определить по следующей формуле:
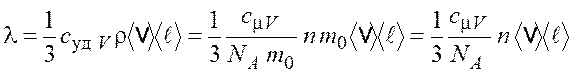 , (20.4)
, (20.4)
где ![]() – удельная теплоемкость при
постоянном объеме;
– удельная теплоемкость при
постоянном объеме; ![]() – плотность;
– плотность; ![]() – средняя скорость молекул;
– средняя скорость молекул; ![]() – средняя длина свободного пробега;
– средняя длина свободного пробега; ![]() – молярная теплоемкость при
постоянном объеме;
– молярная теплоемкость при
постоянном объеме; ![]() – число Авогадро;
– число Авогадро; ![]() – концентрация
молекул;
– концентрация
молекул; ![]() – масса одной молекулы.
– масса одной молекулы.
Молярная теплоемкость при постоянном объеме (считаем воздух идеальным газом)
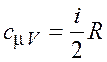 ,
(20.5)
,
(20.5)
где ![]() – сумма числа степеней
свободы поступательного и вращательного движений молекулы,
– сумма числа степеней
свободы поступательного и вращательного движений молекулы, ![]() .
.
Среднюю скорость молекул найдем по формуле
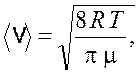 (20.6)
(20.6)
где ![]() – температура воздуха между
стенками,
– температура воздуха между
стенками, ![]() ;
; ![]() –
молярная масса воздуха,
–
молярная масса воздуха, ![]() .
.
Концентрацию молекул найдем из начальных условий
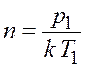 ,
(20.7)
,
(20.7)
Подставив выражения (20.7), (20.6), (20.5), (20.4) в формулу (20.3), получим
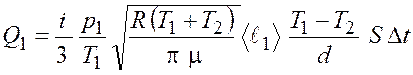 , (20.8)
, (20.8)
Подставив числовые значения и, учитывая, что средняя длина
свободного пробега молекул в первом случае ![]() м,
получим
м,
получим
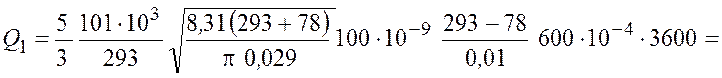
![]()
Во втором случае ![]() .
Следовательно, соударениями молекул друг с другом можно пренебречь и учитывать
только удары молекул о стенки сосуда.
.
Следовательно, соударениями молекул друг с другом можно пренебречь и учитывать
только удары молекул о стенки сосуда.
Для расчета теплоты ![]() , получаемой
холодной стенкой, необходимо знать число ударов
, получаемой
холодной стенкой, необходимо знать число ударов ![]() ,
испытываемых стенкой за время
,
испытываемых стенкой за время ![]() , и энергию
, и энергию ![]() теряемую одной молекулой при ударе,
теряемую одной молекулой при ударе,
![]() . (20.9)
. (20.9)
Можно предположить, что в пространстве между стенками
дюаровского сосуда имеются как бы два встречных потока молекул. Один поток
состоит из молекул, летящих от более нагретой стенки со среднеквадратичной
скоростью ![]() и имеющих среднюю энергию, соответствующую
температуре
и имеющих среднюю энергию, соответствующую
температуре ![]() . Другой поток состоит из молекул, летящих
от холодной стенки со среднеквадратичной скоростью
. Другой поток состоит из молекул, летящих
от холодной стенки со среднеквадратичной скоростью ![]() и
имеющих среднюю энергию, соответствующую температуре
и
имеющих среднюю энергию, соответствующую температуре ![]() .
Среднеквадратичные скорости молекул рассчитываются по следующим формулам:
.
Среднеквадратичные скорости молекул рассчитываются по следующим формулам:
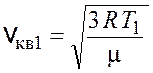 ,
, 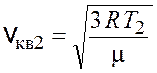 .
(20.10)
.
(20.10)
Молекулы газа подлетают к стенке с одной скоростью, а после взаимодействия со стенкой отлетают с другой скоростью, соответствующей температуре стенки. Механизм изменения скорости выглядит следующим образом. На поверхности каждой стенки существует слой адсорбированных молекул. Температура слоя равна температуре стенок. Этот слой молекул находится в динамическом равновесии с молекулами газа: молекулы из объема газа подлетают к стенке и “прилипают” к ней; одновременно из слоя вылетают, “испаряются” молекулы (происходит реадсорбция молекул) со средней кинетической энергией, соответствующей температуре стенки. Импульс силы, который получает стенка в результате этих двух процессов, будет такой же, как при отражении молекул от стенки, а не как при поглощении. Подлетающую и отлетающую молекулы можно рассматривать как одну молекулу, претерпевшую частично упругий удар о стенку.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.