Явления переноса в газах: Учебно-методическое обеспечение практического занятия, страница 3

Подставим выражения (18.1) – (18.5) в формулу (18.6), выполним преобразования и получим

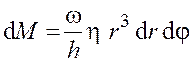.                                   (18.7)

 

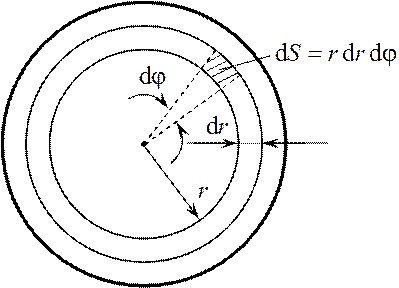Рис. 18.1

Проинтегрировав выражение (18.7) по  от  до  и по  от  до , получим

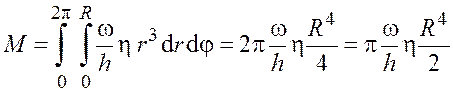.              (18.8)

Подставим числовые значения и получим

.

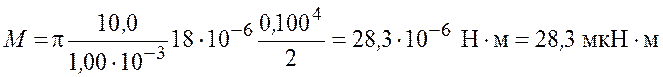Ответ: .

       Пример 4. Пространство между двумя коаксиальными цилиндрами заполнено азотом при давлении 101 кПа и температуре 20,0 °С. Радиусы цилиндров равны 10,0 и 10,5 см. Внешний цилиндр приводят во вращение с частотой 15,0 об/с. Какой момент нужно приложить к внутреннему цилиндру, чтобы он оставался неподвижным? Длина цилиндров 30,0 см.

.                                   (19.1)

Слой молекул газа, адсорбированных внешней поверхностью меньшего неподвижного цилиндра, будет неподвижным, т. е.

.                                             (19.2)

Сила, действующая на боковую поверхность внутреннего цилиндра, определяется по закону Ньютона для вязкости

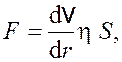                                         (19.3)

где  – градиент направленной скорости;  – коэффициент внутреннего трения азота при заданных условиях;  – площадь боковой поверхности внутреннего цилиндра.

Предполагаем, что направленная скорость газа в пространстве между цилиндрами (на расстоянии  см) изменяется линейно с расстоянием. Тогда градиент направленной скорости можно рассчитать по следующей формуле:

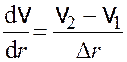.                                       (19.4)

Площадь боковой поверхности цилиндра

.                                        (19.5)

В данных условиях азот можно считать идеальным газом и коэффициент внутреннего трения азота может быть рассчитан по формуле

                                       (19.6)

где  – средняя длина свободного пробега;  – средняя скорость молекул;  – плотность.

Средняя длина свободного пробега молекул азота

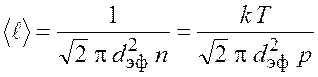,                        (19.7)

где  – эффективный диаметр молекул;  – концентрация молекул; k – постоянная Больцмана; T – термодинамическая температура; p – давление. Эффективный диаметр молекул азота  м.

Средняя скорость молекул

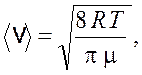                                       (19.8)

где  – температура азота между цилиндрами;  – молярная масса азота, .

Плотность газа найдем, используя уравнение состояния идеального газа,

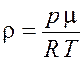.                                           (19.9)

Момент сил, действующий на внутренний цилиндр,

.                                        (19.10)

Подставим выражения (19.1) – (19.9) в формулу (19.10), сделаем преобразования и получим

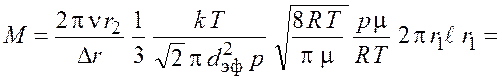
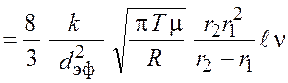.                        (19.11)

Подставим числовые значения и получим

.

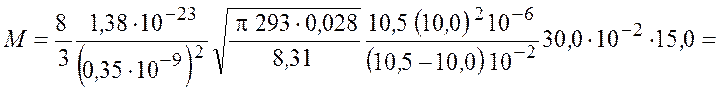
Ответ:  .

        Пример 5. Между стенками дюаровского сосуда находится воздух. Площадь поверхности как внутренних, так и наружных стенок сосуда 600 . Расстояние между стенками 1 см. Температура наружных стенок 20 °С. Температура внутренних стенок 78 К (сосуд заполнен жидким азотом). Какое количество теплоты передается молекулами воздуха от наружных стенок к внутренним за 1 ч. Рассмотреть два случая: 1) давление воздуха до заполнения сосуда жидким азотом было 101 кПа; 2) давление воздуха до заполнения сосуда жидким азотом было 333 мкПа.