Найдем давление, испытываемое холодной стенкой. Импульс
средней силы, получаемый стенкой за время 
(закон
изменения импульса),
,
(17.3)
где 
– изменение импульса
молекулы; 
– количество ударов о стенку.
Изменение импульса молекулы при частично упругом отражении от стенки (предполагается, что скорость молекулы перпендикулярна стенке)
. (17.4)
Вследствие хаотичности движения молекул (равновероятности движения во всех направлениях) можно считать, что от стенки к стенке движется одна треть всех молекул. Поэтому количество ударов о стенку
,
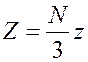(17.5)
где 
– число всех молекул; 
– количество ударов одной молекулы за
время .
Величина может быть получена из
следующего соотношения:
,
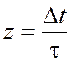(17.6)
где 
– время между двумя
последовательными ударами одной молекулы об одну и ту же стенку. Это время
можно найти следующим образом:
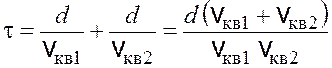. (17.7)
Подставим выражения (17.7), (17.6) в формулу (17.5) и получим количество ударов о стенку
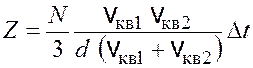. (17.8)
Выражения (17.4) и (17.8) подставим в формулу (17.3) и
получим импульс средней силы, испытываемый стенкой за время ,
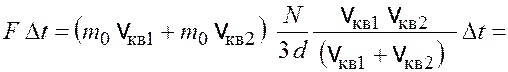
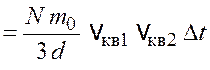. (17.9)
Средняя сила, действующая на стенку,
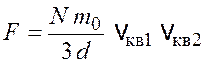. (17.10)
Давление на стенку
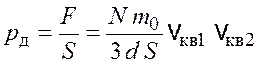, (17.11)
где 
– площадь стенки.
Число всех молекул
, (17.12)
где 
– концентрация
молекул; 
– объем пространства между стенками.
Концентрацию молекул найдем из начальных условий
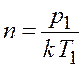, (17.13)
где 
– постоянная Больцмана.
Подставим выражения (17.12), (17.13) и (17.2) в формулу (17.11) и получим
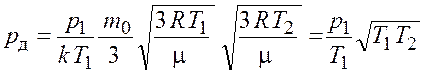. (17.14)
Полученный результат симметричен относительно температур, следовательно, такое же давление будет испытывать и более нагретая стенка.
Подставим числовые значения и получим
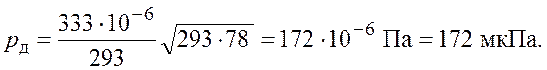
Ответ: 
мкПа.
Пример 3. Два одинаковых параллельных диска, оси
которых совпадают, расположены на расстоянии 1,00 мм друг от друга. Радиус
каждого диска равен 100 мм. Один диск вращается с угловой скоростью
10,0 рад/с, а другой неподвижен. Найти момент сил трения, действующий на
каждый диск, если вязкость воздуха между ними равна 
.
|
Дано: |
Решение |
|
|
В условии задачи неявно предполагается, что упорядоченное
движение слоев воздуха между дисками имеет ламинарный характер (без
турбулентности), и так как |
Слой молекул газа, адсорбированных внутренней поверхностью вращающегося диска, будет обладать той же направленной скоростью, что и диск, т. е.
.
(18.1)
Молекулы газа, адсорбированные внутренней поверхностью неподвижного диска, будут неподвижны, т. е.
.
(18.2)
Сила, действующая на элемент внутренней поверхности диска
площадью 
,
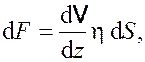(18.3)
где 
– градиент направленной
скорости; 
– коэффициент
внутреннего трения воздуха при заданных условиях.
Площадь элемента внутренней
поверхности диска (рис. 18.1)
.
(18.4)
Предполагаем, что направленная скорость воздуха в пространстве
между дисками (на расстоянии 
мм) изменяется
линейно с расстоянием. Тогда градиент направленной скорости можно рассчитать по
следующей формуле:
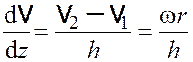. (18.5)
Момент сил, действующий на элемент внутренней
поверхности диска,
.
(18.6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
м;
м;
;
.
–
?
, то краевыми
эффектами можно пренебречь.