Научить студентов применять следующие понятия и законы: Классический гармонический осциллятор. Гармонические колебания. Частота и период колебаний. Фаза колебаний. Затухающие и вынужденные колебания. Логарифмический декремент затухания. Резонанс.
Анализ задач по данной теме начинается с выяснения характера колебательного процесса. Это позволяет написать уравнение, в соответствии с которым движется маятник. Показать, что при незатухающих гармонических колебаниях скорость и ускорение также изменяются во времени по гармоническому закону. Рассмотреть варианты сложения гармонических колебаний и определить характер результирующего колебания. Напомнить, от чего зависит частота собственных колебаний простейших маятников: математического, физического и пружинного. Показать, что кинетическая и потенциальная энергии изменяются с удвоенной частотой. Рассмотреть характер колебаний при наличии сил сопротивления и показать, что частота затухающих колебаний всегда ниже частоты собственных гармонических колебаний. Рассмотреть вынужденные механические колебания и связанные с ними резонансные явления.
[1] 6.1 - 6.7; [7] §3.
Пример 1. Точка совершает
гармонические колебания с частотой ![]() Гц. В момент
времени, принятый за начальный, точка имела максимальное смещение
Гц. В момент
времени, принятый за начальный, точка имела максимальное смещение ![]() мм. Написать уравнение колебаний
точки с числовыми коэффициентами.
мм. Написать уравнение колебаний
точки с числовыми коэффициентами.
|
Дано: |
Решение |
|
|
Первый способУравнение колебаний точки можно записать в виде |
![]() , (23.1)
, (23.1)
где ![]() –
амплитуда колебаний;
–
амплитуда колебаний; ![]() – циклическая частота;
– циклическая частота; ![]() – время;
– время; ![]() –
начальная фаза. По определению амплитуда колебаний
–
начальная фаза. По определению амплитуда колебаний
![]() .
(23.2)
.
(23.2)
Циклическая частота ![]() связана
с частотой
связана
с частотой ![]() соотношением
соотношением
![]() .
(23.3)
.
(23.3)
В момент времени ![]() формула (23.1)
принимает вид
формула (23.1)
принимает вид
![]() ,
,
откуда начальная фаза
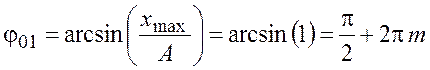 ,
, ![]() .
.
Изменение фазы на ![]() не изменяет значения
колеблющейся величины, поэтому можно принять
не изменяет значения
колеблющейся величины, поэтому можно принять ![]() и тогда
и тогда
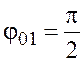 .
(23.4)
.
(23.4)
С учётом равенств (23.2) – (23.4) уравнение колебаний (23.1) примет вид
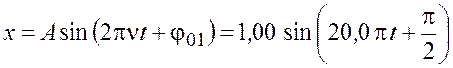 , мм.
, мм.
Второй способ
Уравнение колебаний точки можно записать в виде
![]() . (23.5)
. (23.5)
В момент времени ![]() формула (23.5)
принимает вид
формула (23.5)
принимает вид
![]() ,
,
откуда начальная фаза
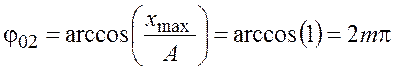 ,
, ![]() .
(23.6)
.
(23.6)
Изменение фазы на ![]() не изменяет значения
колеблющейся величины, поэтому можно принять
не изменяет значения
колеблющейся величины, поэтому можно принять ![]() и тогда
и тогда
![]() .
.
С учётом равенств (23.2), (23.3), (23.6) уравнение колебаний (23.5) примет вид
![]() , мм.
, мм.
Пример 2. Следует сложить два
колебания одинакового направления, выраженные уравнениями: 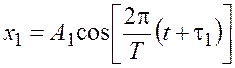 , см, и
, см, и 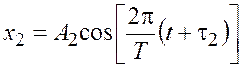 , см,
где
, см,
где ![]() см;
см; ![]() см;
см;
![]() с;
с; ![]() с;
с;
![]() с. В выбранном масштабе произвести
сложение указанных колебаний методом векторных диаграмм в момент времени
с. В выбранном масштабе произвести
сложение указанных колебаний методом векторных диаграмм в момент времени ![]() . Написать уравнение результирующего
колебания с числовыми коэффициентами.
. Написать уравнение результирующего
колебания с числовыми коэффициентами.
|
Дано: |
Решение |
|
|
Преобразуем уравнения
Сравним их с уравнением, записанным в канонической
форме, |
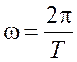 .
.
Начальные фазы первого и второго колебаний соответственно равны
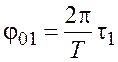 ;
;
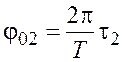 .
.
Произведём вычисления
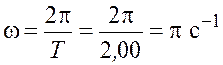 ;
;
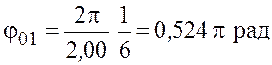 ;
;
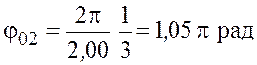 .
.
Таким образом, исходные колебания происходят по законам
![]() , см;
, см;
![]() , см.
, см.
Поскольку складываются гармонические колебания одного направления и одинаковой частоты, результирующее колебание является гармоническим, совершается в том же направлении и имеет ту же частоту, что и слагаемые колебания. Уравнение результирующего колебания можно записать в виде
![]() .
.
Для построения векторной диаграммы сложения двух колебаний
одного направления нужно фиксировать какой-либо момент времени. Обычно
векторную диаграмму строят для момента времени ![]() .
.
Изобразим на рис. 24.1 векторы ![]() и
и
![]() , длина которых равна амплитуде колебаний.
Для этого отложим отрезки длиной
, длина которых равна амплитуде колебаний.
Для этого отложим отрезки длиной ![]() см и
см и ![]() см под углом
см под углом ![]() º
и
º
и ![]() º к оси
º к оси ![]()
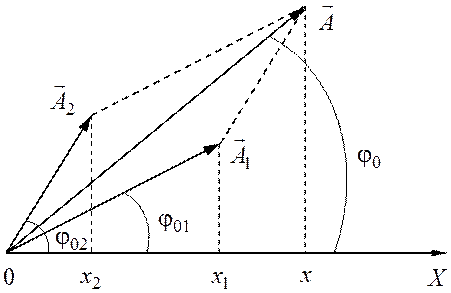 |
Рис. 1
Результирующее колебание будет происходить с той же частотой
![]() , что и складываемые колебания. Вектор
, что и складываемые колебания. Вектор ![]() , длина которого равна амплитуде
результирующего колебания, равен векторной сумме
, длина которого равна амплитуде
результирующего колебания, равен векторной сумме ![]() и
и ![]()
![]() .
.
Согласно теореме косинусов
![]() .
.
Начальную фазу результирующего колебания можно также определить непосредственно из векторной диаграммы (см. рис. 1).
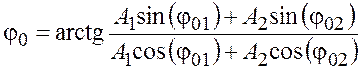 .
.
Произведём вычисления
![]() см;
см;
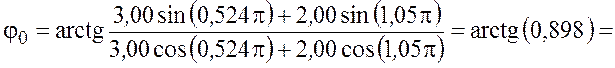
= 0,735 рад.
Таким образом, уравнение результирующего колебания можно записать в виде
![]() , см.
, см.
Пример 3. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых
![]() , см
, см ![]() , см
, см
где ![]() см;
см; ![]() ;
;
![]() см;
см; ![]() . Найти
уравнение траектории точки
. Найти
уравнение траектории точки ![]() . Построить траекторию с
соблюдением масштаба и указать направление движения точки.
. Построить траекторию с
соблюдением масштаба и указать направление движения точки.
|
Дано: |
Решение |
|
|
Чтобы определить траекторию точки, исключим время из уравнений (25.1) и (25.2)
Заметив, что |
применим формулу косинуса половинного угла для выражения (25.2)
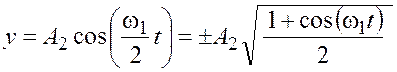 . (25.3)
. (25.3)
Из выражения (25.1) получим
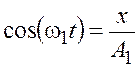 .
(25.4)
.
(25.4)
Подставим выражение (25.4) в уравнение (25.3)
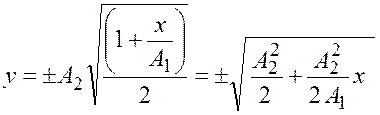 .
.
После подстановки численных значений получим
![]() , см.
(25.5)
, см.
(25.5)
Последнее уравнение представляет собой уравнение параболы,
ось которой совпадает с осью X. Как показывают
уравнения (25.1) и (25.2), амплитуда колебаний точки по оси X равна 1,00 см, а
по оси Y – 2,00 см. Следовательно, абсциссы всех точек траектории заключены
в пределах от –1,00 до 1,00 см, а ординаты – от –2,00 до 2,00 см.
Для построения траектории найдем по уравнению (25.5) значения ![]() , соответствующие ряду значений
, соответствующие ряду значений ![]() , удовлетворяющих условию
, удовлетворяющих условию ![]() см:
см:
|
|
|
|
|
|
–1,00 |
0 |
0 |
|
|
–0,750 |
|
0,500 |
|
|
–0,500 |
|
1,00 |
|
Начертив координатные оси и выбрав единицу длины – сантиметр,
построим точки. Соединив их плавной кривой, получим траекторию результирующего
колебания точки (рис. 25.1). Она представляет собой часть параболы, заключенной
внутри прямоугольника амплитуд ABCD. В начальный
момент (![]() ) имеем
) имеем ![]() см,
см,
![]() см (точка находится в положении
см (точка находится в положении ![]() ). При
). При ![]() с
получим
с
получим ![]() см и
см и ![]() см
(точка находится в положении D). После этого она
будет двигаться в обратном направлении.
см
(точка находится в положении D). После этого она
будет двигаться в обратном направлении.
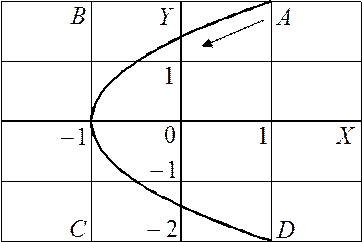 |
Рис. 25.1
Пример 4. Частица массой ![]() г совершает гармонические колебания с
периодом
г совершает гармонические колебания с
периодом ![]() с. Полная энергия колеблющейся
частицы
с. Полная энергия колеблющейся
частицы ![]() мкДж. Определить амплитуду колебаний
и наибольшее значение силы
мкДж. Определить амплитуду колебаний
и наибольшее значение силы ![]() , действующей на
частицу.
, действующей на
частицу.
|
Дано: |
Решение |
|
|
Для определения амплитуды колебаний воспользуемся выражением для полной энергии частицы
где |
Отсюда амплитуда
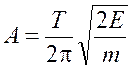 .
(26.1)
.
(26.1)
Так как частица совершает гармонические колебания, то сила,
действующая на нее, является квазиупругой и, следовательно, может быть выражена
соотношением ![]() , где
, где ![]() –
коэффициент квазиупругой силы;
–
коэффициент квазиупругой силы; ![]() – смещение колеблющейся
точки. Максимальной сила будет при максимальном смещении
– смещение колеблющейся
точки. Максимальной сила будет при максимальном смещении ![]() , равном амплитуде
, равном амплитуде ![]() ,
,
![]() .
(26.2)
.
(26.2)
Коэффициент ![]() выразим через период
колебаний
выразим через период
колебаний
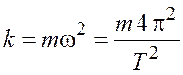 .
(26.3)
.
(26.3)
Подставив выражение (26.1) и (26.3) в (26.2) и произведя упрощения, получим
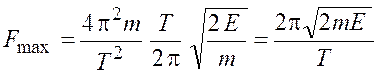 . (26.4)
. (26.4)
Произведём вычисления
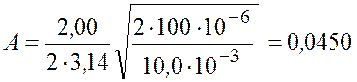 м = 45,0 мм;
м = 45,0 мм;
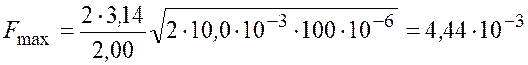 Н = 4,44 мН.
Н = 4,44 мН.
Пример 5. Гиря массой ![]() г подвешена к пружине, коэффициент
жёсткости которой
г подвешена к пружине, коэффициент
жёсткости которой ![]() Н/м, и совершает затухающие
колебания. Определить их период, если за время двух колебаний (
Н/м, и совершает затухающие
колебания. Определить их период, если за время двух колебаний (![]() ) амплитуда уменьшилась в
) амплитуда уменьшилась в ![]() раз. Записать дифференциальное
уравнение затухающих колебаний с числовыми коэффициентами.
раз. Записать дифференциальное
уравнение затухающих колебаний с числовыми коэффициентами.
|
Дано: |
Решение |
|
|
Дифференциальное уравнение затухающих колебаний имеет вид
где |
Для записи уравнения необходимо найти значения ![]() и
и ![]() .
.
Циклическая частота собственных колебаний пружинного маятника
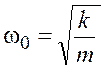 .
(27.2)
.
(27.2)
Амплитуда затухающих колебаний для двух моментов времени
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.