Электрическая емкость. Энергия электростатического поля: Учебно-методическое обеспечение практического занятия

сами заряженные проводники, так и созданное им электростатическое поле. Однако здесь же следует указать, что электродинамика показывает о распределении энергии в электрическом поле. Вычислить объемную плотность энергии поля.

Целесообразно везде, где это возможно, пользоваться законом сохранения и превращения энергии.

3.3.3. Рекомендуемая литература

[3] 2.8, 3.5,§24-30.

3.3.4. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

Пример 1. Плоский воздушный конденсатор с площадью пластин 100  и расстоянием между ними 1,00 мм заряжен до 100 В. Пластины раздвигают до расстояния 25,0 мм. Найти энергию конденсатора до и после раздвижения пластин, если источник напряжения перед раздвижением: 1) не отключается; 2) отключается.

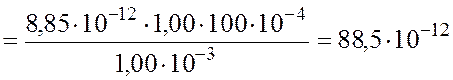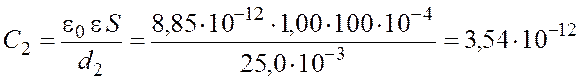              Ф;

   Ф.

1. Источник напряжения не отключается. Напряжение до и после раздвижения пластин в этом случае будет оставаться одинаковым:

                                         .

Энергия конденсатора до и после раздвижения:

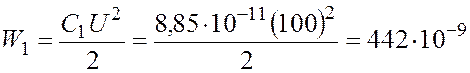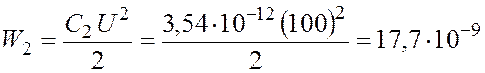           Дж;

          Дж.

2. Источник напряжения отключается. В этом случае заряд на конденсаторе остается неизменным до и после раздвижения пластин, но изменится напряжение:

                           ;          .

Так как , то , откуда

                 .

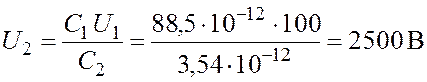Энергия конденсатора после раздвижения пластин

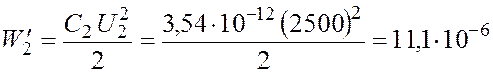         Дж.

Ответ: 1)  Дж;  Дж;

 2)  Дж.

Пример 2. Конденсатор, обладающий электрической емкостью  мкФ, был заряжен до разности потенциалов  В. После отключения от источника тока конденсатор соединили параллельно с другим, незаряженным конденсатором электрической емкостью  мкФ. Какая энергия будет израсходована на образование искры в момент присоединения второго конденсатора?

Дано:	Решение
мкФ;  мкФ;  В;  В.  – ?	Энергия образования искры возникает из-за уменьшения полной энергии электрического поля системы: ,                (2.1)

где  – энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора;  – энергия, которую имеет система, составленная из двух конденсаторов.

Энергия заряженного конденсатора определяется по формуле

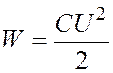                                           ,                                            (2.2)

где  – электрическая емкость конденсатора или общая электрическая емкость системы конденсаторов.

Общая электрическая емкость конденсаторов при параллельном включении

                                          .

Подставив в формулу (2.1)  и , по формуле (2.2) получим

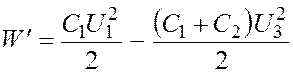                            ,                             (2.3)

где  – разность потенциалов на зажимах батареи конденсаторов.

Систему, состоящую из двух конденсаторов, отключенных от источника, можно считать электрически изолированной. Поэтому суммарный заряд после присоединения второго конденсатора остался прежним. Выразим разность потенциалов  следующим образом:

                               ;                               (2.4)

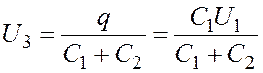                               .                               (2.5)

Подставив выражение (2.5) в (2.3), найдем

        

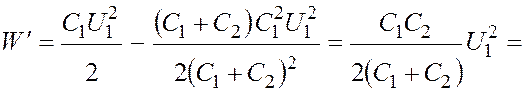
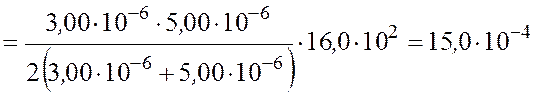     Дж.

Ответ:  Дж.

Пример 3. Плоский конденсатор, между обкладками которого помещена стеклянная пластинка () толщиной  мм, заряжен до разности потенциалов  В. Пренебрегая величиной зазора между пластинкой и обкладками, найти поверхностную плотность свободных зарядов на обкладках конденсатора, а также поверхностную плотность связанных зарядов на стекле.

Дано:	Решение
мм м;  В; .  – ?  – ?	Величину  можно выразить через напряженность поля внутри конденсатора: .

Учитывая соотношение, справедливое для однородного поля конденсатора, можно записать:

                                           .

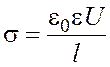Чтобы определить величину , воспользуемся формулой связи с вектором поляризации:

                                       .

Поскольку , можно записать

                           .

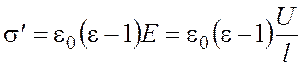          После подстановки численных значений получим

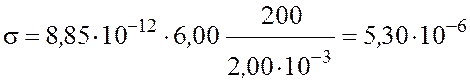         Кл/м²;

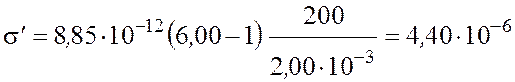     Кл/м².

Ответ:  Кл/м²;  Кл/м².

3.3.5. Задачи для решения на практических
занятиях

1. Плоскому конденсатору с квадратными пластинами сообщен заряд  нКл. Сторона пластины  см. Найти напряженность поля в центре конденсатора. Какая сила будет действовать на заряд  нКл, расположенный в конденсаторе?

2. Напряженность поля заряженного плоского конденсатора с расстоянием между пластинами  см равна  В/см. Параллельно пластинам в конденсатор вносится незаряженная металлическая пластина толщиной  см. Найти разность потенциалов между пластинами конденсатора до и после внесения металлической пластины.

3. Конденсаторы, емкости которых  мкФ,  мкФ, и  мкФ, включены в цепь напряжением  В. Определить заряды и разность потенциалов на обкладках конденсаторов в случае их последовательного и параллельного включения.

4. Между пластинами плоского конденсатора находятся два слоя диэлектрика: слюдяная пластинка () толщиной  мм и парафин () толщиной  мм. Определить напряженность электростатических полей в слоях диэлектрика, если разность потенциалов между пластинами конденсатора  В.

5. Два проводящих шара, заряженных до потенциалов соответственно  В и  В, находятся на таком большом расстоянии друг от друга, что их можно считать уединенными. Электрические емкости шаров  мкФ и  мкФ. Какими будут заряды на шарах, если их соединить тонким проводником, имеющим пренебрежимо малую электрическую емкость по сравнению с электрической емкостью шаров? Каким станет потенциал каждого из шаров?

6. Плоский воздушный конденсатор емкостью  пФ заряжен до разности потенциалов  В. После отключения конденсатора от источника напряжения расстояние между пластинами конденсатора было увеличено в три раза. Определить разность потенциалов на обкладках конденсатора после их раздвижения, а также работу внешних сил по раздвижению пластин.

7. Два конденсатора емкостями  мкФ и  мкФ соединили последовательно и зарядили до разности потенциалов  кВ. Как изменится энергия системы, если ее отключить от источника напряжения и одноименные заряженные обкладки конденсаторов соединить параллельно