Показать студентам, что свойства реальных газов существенным образом отличаются от свойств идеальных газов. При этом уравнение состояния должно учитывать давление, обусловленное силами межмолекулярного взаимодействия и собственный объём молекул. Показать, как определяются поправочные коэффициенты в уравнении Ван-дер Вальса и от чего они зависят.
При решении задач по данному разделу обратить внимание на границы применимости уравнения состояния идеального газа. Показать, что каждое реальное вещество, независимо от его молекулярной структуры может существовать по крайней мере в трёх агрегатных состояниях. Для каждого вещества критические параметры и параметры, соответствующие тройной точке сугубо индивидуальны. Поэтому постоянные Ван-дер-Ваальса «а» и «b» также являются индивидуальными для каждого вещества. При этом параметры в критической точке оказываются однозначно связанными с постоянными Ван-дер-Ваальса.
[2] , Т.2, гл. 7, [6] 4.9.
Пример 1. В сосуде емкостью 20,0 л при
температуре 310 К находится 4,00 кг углекислого газа ![]() . Найти давление газа на стенки сосуда.
. Найти давление газа на стенки сосуда.
|
Дано: |
Решение |
|
|
Найдем давление, которое оказывал бы газ, если бы подчинялся уравнению Клапейрона–Менделеева,
Откуда |
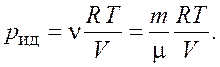
Подставим числовые значения и получим
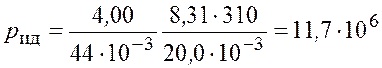 Па.
Па.
Полученное давление настолько велико, что применение уравнения идеального газа вряд ли оправдано. Рассчитаем давление по уравнению Ван-дер-Ваальса
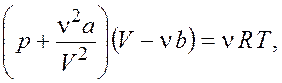
где ![]() ,
, ![]() –
постоянные Ван-дер-Ваальса. Для углекислого газа
–
постоянные Ван-дер-Ваальса. Для углекислого газа
![]()
![]()
Откуда
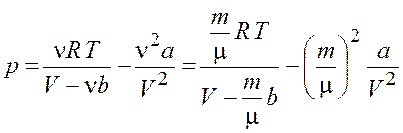 .
.
Подставим числовые значения и получим
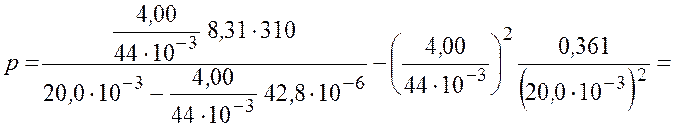
![]() МПа.
МПа.
Тот факт, что давление углекислого газа оказалось меньше, чем давление идеального газа, показывает, что доминирующей является поправка на силы притяжения, чем на силы отталкивания (собственный объем молекул)
Ответ: ![]() МПа.
МПа.
Пример 2. В сосуде емкостью 20,0 л при
температуре 300 К находится 182 г водорода ![]() . Найти давление газа на стенки сосуда.
. Найти давление газа на стенки сосуда.
|
Дано: |
Решение |
|
|
Найдем давление, которое оказывал бы газ, если бы подчинялся уравнению Клапейрона–Менделеева,
Откуда |
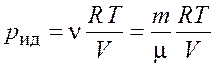 .
.
Подставим числовые значения и получим
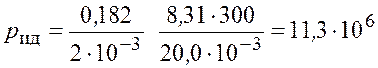 Па.
Па.
Полученное давление настолько велико, что применение уравнения идеального газа вряд ли оправдано. Рассчитаем давление по уравнению Ван-дер-Ваальса
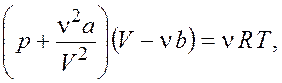
где ![]() ,
, ![]() –
постоянные Ван-дер-Ваальса. Для водорода
–
постоянные Ван-дер-Ваальса. Для водорода
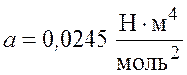 ,
, 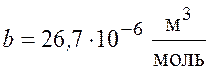 .
.
Откуда
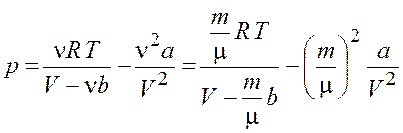 .
.
Подставим числовые значения и получим
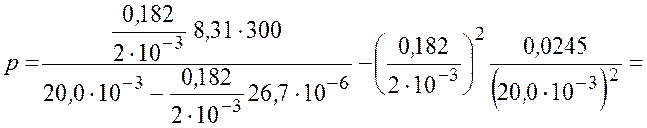
![]() МПа.
МПа.
Тот факт, что давление водорода оказалось больше, чем давление идеального газа, показывает, что доминирующей является поправка на силы отталкивания (собственный объем молекул), чем на силы притяжения.
Ответ: ![]() МПа.
МПа.
1. Азот массой 2,00г занимает объём 82,0 см3 при давлении в 2,02 МПа. Найти температуру газа, рассматривая его как: 1) идеальный; 2) Ван-дер-ваальсовский.
2. Кислород имеет плотность 129кг/м3 при давлении 7,25 МПа. Найти температуру газа: 1) по уравнению Менделеева-Клапейрона; 2) по уравнению Ван-дер-Ваальса.
3. Найти плотность гелия в критическом состоянии, считая известными для гелия значения критических величин Тк и рк.
4. В сосуде вместимостью 10,0 л находится азот массой 250 г. Найти давление, обусловленное силами взаимодействия молекул и их собственный объём.
5. Найти эффективный диаметр молекулы азота двумя способами: 1) по данному значению средней длины свободного пробега молекул при нормальных условиях, равному 95,0 нм; 2) по известной величине постоянной b уравнении Ван-Дер-Ваальса.
6. Газ находится в критическом состоянии. Во сколько раз возрастёт давление газа, если его температуру изохорно увеличить в 3,00 раза? Задачу решить для двух случаев: 1) газ идеальный; 2) газ ван-дер-ваальсовский.
4.9.2, 4.9.5, 4.9.6, 4.9.10, 4.9.15, 4.9.23.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.