Прямые и обратные циклы. Энтропия: Учебно-методическое обеспечение практического занятия

2.3. Прямые и обратные циклы. Энтропия (6 часов)

2.3.1. Учебная цель занятиий

Научить студентов применять следующие понятия и законы: Второе начало термодинамики. Принцип действия тепловой и холодильной машин. Цикл (круговой процесс) и его КПД. Цикл Карно, теорема Карно. Энтропия.

2.3.2. Методические указания к проведению занятий

Задачи данного раздела посвящены применению первого начала термодинамики к замкнутым процессам (циклам), причём все процессы протекают в идеальном газе. При этом предполагается, что процессы, составляющие цикл, являются квазистатическими (все промежуточные состояния равновесны). Это позволяет записывать уравнение первого начала в интегральной форме. Показать, что использование дифференциальной записи первого начала термодинамики целесообразно в тех случаях, когда с помощью этого закона и уравнения состояния нужно найти уравнение изопроцесса или теплоемкости газа при различных изопроцессах.

Анализ задач начинается с графического изображения циклов. Для лучшего понимания рассматриваемых явлений важно привлекать молекулярно-кинетические представления. При решении задач использовать выражение коэффициента полезного действия тепловой машины и холодильного коэффициента для холодильных машин, в том числе  и для цикла Карно.

Произвести вычисление изменения энтропии при обратимых процессах в идеальном газе и подчеркнуть на этих примерах, что энтропия в отличие от количества теплоты и работы является функцией состояния.

2.3.3. Рекомендуемая литература

[2] §2.1-2.8; 5.1-5.12  [6] стр. 271-277.

2.3.4. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

Пример 1. Идеальный газ, совершающий цикл Карно, 70 % количества теплоты , полученной от нагревателя, отдает холодильнику. Количество теплоты, полученное от нагревателя, равно 5,00 кДж. Определить термический КПД цикла , работу, совершаемую в цикле .

С другой стороны, КПД цикла можно выразить через работу , совершаемую рабочим телом за цикл,

.

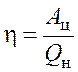Отсюда

.

Ответ: , .

Пример 2. Идеальная тепловая машина работает по циклу Карно. Температура холодильника ниже температуры нагревателя на 20 %. Какую работу совершает машина за один цикл, если при этом она получает   = 6000 Дж теплоты ?

Дано:	Решение
= 20 %;  = 6000 Дж.  – ?	Выразим соотношение между температурами нагревателя и холодильника в относительных единицах .

С другой стороны, КПД идеальной тепловой машины

.

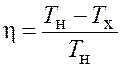Сравнивая эти два выражения, получим

.

КПД, измеряемое в процентах, определяется формулой

,

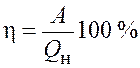откуда

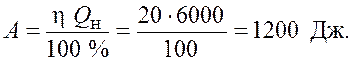
Ответ:  = 1200 Дж.

Пример 3. Тепловая машина работает по циклу Карно. Температура нагревателя . Определить термический КПД цикла и температуру  холодильника тепловой машины, если за счет каждого килоджоуля теплоты, полученной от нагревателя, машина совершает работу .

где  – теплота, полученная от нагревателя;  – работа, совершенная рабочим телом тепловой машины.

Зная КПД цикла, можно по формуле  определить температуру холодильника

.

Произведем вычисления

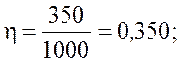
Ответ: , .

Пример 4. Гелий  массой  в качестве рабочего тела используется в прямом цикле, состоящем из двух изобар, адиабаты и изохоры. В начальном состоянии гелий занимает объем  при давлении . При изобарном нагревании объем газа увеличивается в два раза, а затем газ адиабатно расширяется, в результате чего его температура уменьшается на . Затем газ изобарно охлаждают до первоначального объема и изохорно повышают давление до первоначального значения. Изобразить цикл в – координатах. Определить температуры характерных точек цикла, КПД цикла .

Количество вещества в рабочем теле

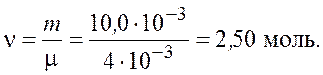
Графическое изображение цикла дано на рис. 4.1.

 

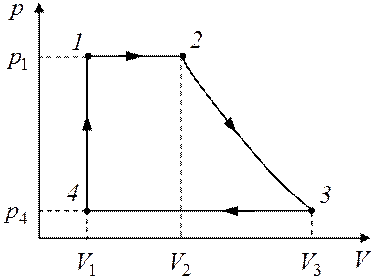Рис. 4.1

Температуру газа в начальном состоянии найдем из уравнения Клапейрона–Менделеева

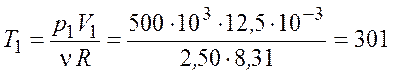 К.

Температуры и объемы в изобарном процессе 1–2 связаны следующим соотношением:

,

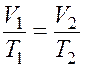откуда и находим температуру

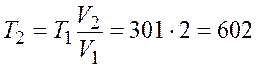 К.

Температура  в точке 3

 К.

Температуры и давления в адиабатном процессе 2–3 связаны следующим соотношением:

.

Давление  в точке 3

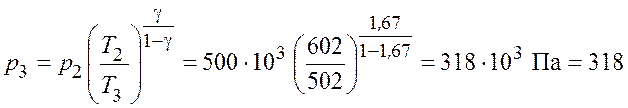 кПа.

Давление  и объем  в точке 4

 кПа,                 

Температуру газа в точке 4 найдем из уравнения Клапейрона–Менделеева

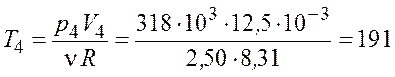 К.

КПД цикла

,

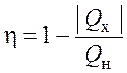где  – теплота, отданная рабочим телом холодильнику;  – теплота, переданная от нагревателя рабочему телу.

Теплота  в изобарном процессе 1–2

 кДж.

Теплота  в адиабатном процессе 2–3 .

Теплота  в изобарном процессе 3–4

 кДж.

Теплота  в изохорном процессе 4–1

 кДж.

Если теплота положительная, то она передается от нагревателя рабочему телу, следовательно,

 кДж.

Если теплота отрицательная, то она передается от рабочего тела холодильнику, следовательно,

 кДж.

На рис. 4.2 показано, в каких процессах осуществляется подвод теплоты от нагревателя и ее отвод к холодильнику.

КПД цикла

.

 

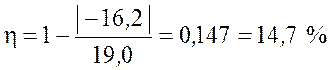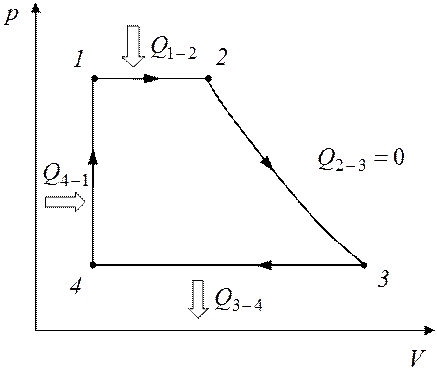
Рис. 4.2

Ответ:  К,   К,   К,   К,

.

Пример 5. Мощность двигателя автомобиля 50,0 кВт. Расход бензина на 100 км пути равен 9,00 кг. С какой скоростью движется автомобиль, если КПД двигателя 60 %? Удельная теплота сгорания бензина 46,0 МДж/кг.