Физика \ Физика

Прямые и обратные циклы. Энтропия: Учебно-методическое обеспечение практического занятия, страница 2

Полезная работа, совершенная двигателем при движении с постоянной скоростью,

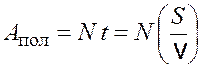,                                  (5.2)

где   – время прохождения пути S;  – скорость движения.

Затраченная двигателем теплота

,                                       (5.3)

где   – удельная теплота сгорания бензина;  – масса бензина, израсходованного на пути .

Подставляя соотношения (5.2) и (5.3) в формулу (5.1), получим

,

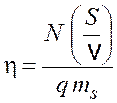откуда скорость автомобиля

.

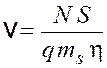Произведем вычисления

.

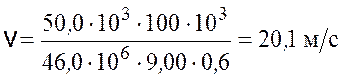Ответ: .


Пример 6. Найти приращение энтропии 10,5 г водорода при изохорном нагревании от 300 до 450 К. Газ считать идеальным.

Дано:

Решение

 К;

 К;

 кг;

 кг/моль.

 – ?

При изохорном квазистатическом нагревании изменение энтропии определяется следующей формулой:

,

где  – молярная теплоемкость при постоянном объеме, .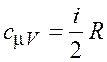

У водорода суммарное число степеней свободы поступательного и вращательного движений .

Подставим числовые значения и получим изменение энтропии

.

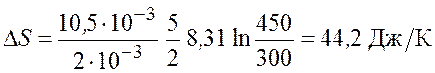Ответ: .


Пример 7 Найти приращение энтропии 10,5 г водорода при переходе от объема 25,6 л  при давлении 175 кПа к объему 78,6 л при давлении 101 кПа. Газ считать идеальным.

Дано:

Решение

;

 Па;

;

 Па;

 кг;

 кг/моль.

 – ?

Изменение энтропии при обратимом квазистатическом переходе из одного состояния в другое определяется только параметрами этих состояний и не зависит от процесса. Из условия задачи характер процесса неизвестен, поэтому переведем идеальный газ из первого состояния во второе с помощью обратимых квазистатических изопроцессов, например, выберем изобарное расширение от объема  до  при давлении  и изохорное изменение давления от  до  в объеме .

Изменение энтропии при обратимом квазистатическом переходе из состояния 1 в состояние 2

,

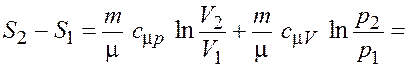
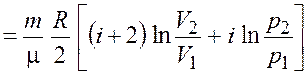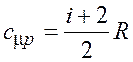где  – молярная теплоемкость при постоянном давлении, ;   – молярная теплоемкость при постоянном объеме, 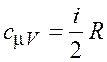;   – суммарное число степеней свободы поступательного и вращательного движений, у водорода .

Подставим числовые значения и получим

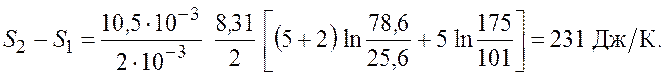
Ответ:


Пример 8. Адиабатно изолированный цилиндр разделен на две равные части теплоизолирующей перегородкой. Идеальный газ в количестве 2,00 моль занимает одну из этих половин. Перегородку внезапно убирают, и газ занимает весь цилиндр. Найти изменение энтропии газа.

Дано:

Решение

;

 моль.

 – ?

Процесс расширения газа в пустоту происходит адиабатно, но не квазистатически. Поэтому применить уравнение адиабатного процесса к начальному и конечному состояниям нельзя.

В ходе расширения газа в пустоту он не совершает никакой работы, и теплота к нему не подводится, следовательно, внутренняя энергия газа остается без изменения. Согласно закону Джоуля внутренняя энергия идеального газа зависит только от температуры. Таким образом, можно заключить, что температура газа осталась такой же, какой была в начале процесса.

Скачать файл