Научить студентов применять следующие понятия и законы: Термодинамическая система. Термодинамические параметры состояния: давление, объем, температура. Термодинамический процесс и его изображение на термодинамической диаграмме.
Молекулярно-кинетическая теория идеального газа. Основное уравнение молекулярно-кинетической теории идеального газа. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона). Смесь газов, парциальное давление. Закон Дальтона.
На занятиях следует остановиться на следующих вопросах: молекулярно-кинетическая трактовка давления, кинетическая энергия хаотического движения молекул. Следует обратить внимание, что основное уравнение молекулярно-кинетической теории выводится из упрощенной модели идеального газа. Подчеркнуть, что действительное распределение по составляющим скоростей заменяется предположением, что молекулы движутся только в трех взаимно перпендикулярных направлениях. Распределение молекул по модулю скорости заменяется предположением о равенстве модуля скорости у всех молекул. В процессе установления равновесия существенная роль принадлежит столкновению молекул. После того, как равновесное состояние установилось, столкновения уже не могут изменить ни распределения скоростей, ни давления, ни температуры, ни других характеристик системы. Нужно отметить, что свойства огромной совокупности молекул отличны от свойств каждой отдельной молекулы и их движении обладает специфическими закономерностями. Свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и средними значениями динамических характеристик этих частиц. Именно при решении задач удобно показать, что уравнение Менделеева-Клапейрона можно рассматривать как следствие основного уравнения кинетической теории идеального газа. Показать, что в уравнении Менделеева-Клапейрона содержатся все частные газовые законы, характеризующие изопроцессы.
[2] §1.1-1.8; [6] стр. 261-263.
Пример 1. Найти массу воздуха, заполняющего аудиторию
высотой ![]() м и площадью пола
м и площадью пола ![]() . Давление воздуха
. Давление воздуха ![]() Па,
температура
Па,
температура ![]() . Молярную массу воздуха принять равной
0,029 кг/моль.
. Молярную массу воздуха принять равной
0,029 кг/моль.
|
Дано: |
Решение |
|
|
Уравнение состояния идеального газа (уравнение Менделеева–Клапейрона)
Объем помещения
|
Из уравнения (1.1) с учетом выражения (1.2) получим
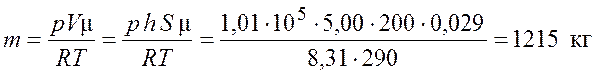 .
.
Ответ: ![]() = 1215 кг.
= 1215 кг.
Пример 2. В баллоне находилось 10,0 кг газа при давлении 10,0 МПа. Найти, какую массу газа взяли из баллона, если окончательное давление стало равно 2,50 МПа. Температуру газа считать постоянной.
|
Дано: |
Решение |
|
|
Запишем уравнение состояния идеального газа (уравнение Менделеева–Клапейрона) для первоначальной и конечной масс газа |
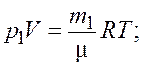 (2.1)
(2.1)
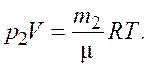 (2.2)
(2.2)
Разделим уравнение (2.1) на уравнение (2.2)
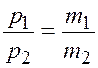 ,
,
откуда масса оставшегося в баллоне газа
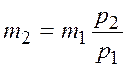 .
.
Масса газа, который взяли из баллона, равна разности масс
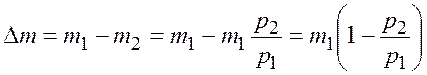 .
.
Подставим числовые значения и получим
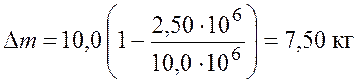 .
.
Ответ: ![]() кг.
кг.
Пример 3. Сосуд объемом 2,00 л заполняют
6,00 г углекислого газа (![]() ) и 5,00 г закиси
азота (
) и 5,00 г закиси
азота (![]() ). Каково общее давление смеси в сосуде при
температуре
). Каково общее давление смеси в сосуде при
температуре ![]() ?
?
|
Дано: |
Решение |
|
|
Из периодической таблицы Менделеева найдем относительные атомные массы элементов, входящих в молекулы указанных газов, и по ним найдем молярные массы газов. |
Для ![]()
![]() .
.
Для ![]()
![]() .
.
Запишем уравнение состояния идеального газа (уравнение Менделеева–Клапейрона) для обоих компонентов смеси
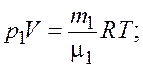 (3.1)
(3.1)
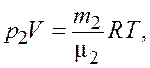 (3.2)
(3.2)
где ![]() ,
, ![]() –
парциальные давления обоих компонентов смеси;
–
парциальные давления обоих компонентов смеси; ![]() –
весь объем сосуда.
–
весь объем сосуда.
Из уравнений (3.1) и (3.2) получим формулы для парциальных давлений
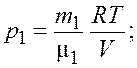 (3.3)
(3.3)
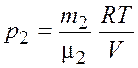 . (3.4)
. (3.4)
По закону Дальтона давление смеси идеальных газов
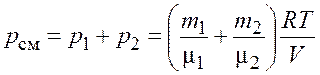 .
.
Подставим числовые значения и получим
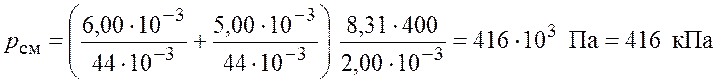 .
.
Ответ: ![]() кПа.
кПа.
Пример 4. Два сосуда, наполненных воздухом при давлении 800 и 600 кПа, имеют соответственно объемы 3,00 и 5,00 л. Сосуды соединяют трубкой, объемом которой можно пренебречь по сравнению с объемом сосудов. Найти установившееся давление в сосудах. Температуру считать постоянной.
|
Дано: |
Решение |
|
|
Поскольку процесс смешения газов происходит при постоянной температуре, запишем закон Бойля–Ма-риотта для обоих компонентов
|
где ![]() и
и ![]() – парциальные давления компонентов смеси;
– парциальные давления компонентов смеси; ![]() – суммарный
объем сосуда, который заполняет каждый компонент.
– суммарный
объем сосуда, который заполняет каждый компонент.
Из уравнений (4.1) и (4.2) найдем парциальное давление
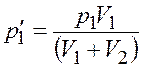 ;
;
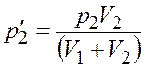 .
.
По закону Дальтона давление смеси идеальных газов
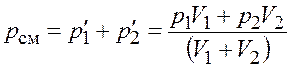 .
.
Подставим числовые значения и получим
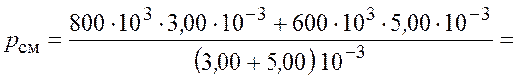
![]() .
.
Ответ: ![]() = 675 кПа.
= 675 кПа.
Пример 5. В баллоне объемом ![]() находится
гелий
находится
гелий ![]() под давлением
под давлением ![]() и при
температуре
и при
температуре ![]() . После того, как из баллона было взято
. После того, как из баллона было взято ![]() гелия, температура в баллоне понизилась до
гелия, температура в баллоне понизилась до
![]() . Определить давление
. Определить давление ![]() гелия, оставшегося в баллоне.
гелия, оставшегося в баллоне.
|
Дано: |
Решение |
|
|
Запишем уравнение Менделеева–Клапейрона для начального и конечного состояния газа
Из уравнения (5.1) выразим массу газа в начальном состоянии |
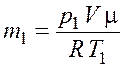 .
(5.3)
.
(5.3)
Тогда масса ![]() оставшегося в баллоне
газа
оставшегося в баллоне
газа
![]() .
(5.4)
.
(5.4)
Из уравнения (5.2) найдем давление газа в конечном состоянии
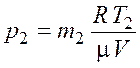 .
(5.5)
.
(5.5)
Подставив выражение (5.3) для массы ![]() в
формулу (5.4), а затем выражение (5.4) для
в
формулу (5.4), а затем выражение (5.4) для ![]() в
уравнение (5.5), получим
в
уравнение (5.5), получим
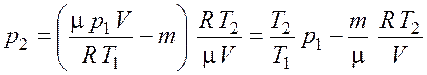 . (5.6)
. (5.6)
Произведем вычисления по формуле (5.6)
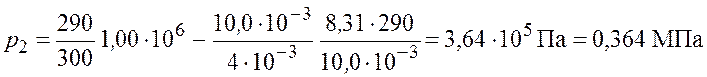 .
.
Ответ: ![]() .
.
Пример 6. Баллон содержит ![]() кислорода
кислорода
![]() и
и ![]() аргона
аргона
![]() . Давление смеси
. Давление смеси ![]() ,
температура
,
температура ![]() . Принимая данные газы за идеальные,
определить объем
. Принимая данные газы за идеальные,
определить объем ![]() баллона.
баллона.
|
Дано: |
Решение |
|
|
По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. По уравнению Клапейрона–Менделеева парциальные давления
|
Следовательно, по закону Дальтона давление смеси газов
![]() или
или 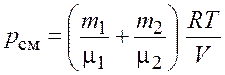 .
.
Откуда объем баллона
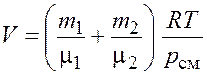 .
.
Произведем вычисления
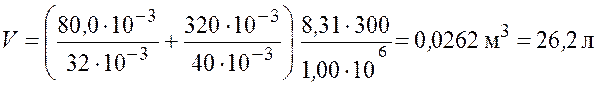 .
.
Ответ: ![]() .
.
Пример 7. В сосуде емкостью 4,00 л находится
1,00 г водорода. Какое число молекул содержится в ![]() этого
газа?
этого
газа?
|
Дано: |
Решение |
|
|
Число молекул в объеме
где Концентрация молекул во всем сосуде
|
Подставив выражение (7.2) в формулу (7.1), получим
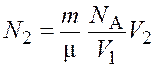 .
.
Подставим числовые значения и получим
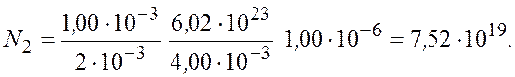
Ответ: ![]()
Пример 8. Определить число ![]() молекул,
содержащихся в объеме
молекул,
содержащихся в объеме ![]() воды, и массу
воды, и массу ![]() одной молекулы воды. Найти эффективный
диаметр
одной молекулы воды. Найти эффективный
диаметр ![]() молекулы, считая, что молекулы воды имеют
вид шариков, соприкасающихся друг с другом и упакованных слоями толщиной
молекулы, считая, что молекулы воды имеют
вид шариков, соприкасающихся друг с другом и упакованных слоями толщиной ![]() .
.
|
Дано: |
Решение |
|
|
Число
Так как
|
Выразив в этой формуле массу как произведение плотности ![]() на объем V, получим
на объем V, получим
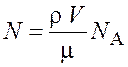 .
.
Рассчитаем число молекул, учитывая, что плотность воды ![]()
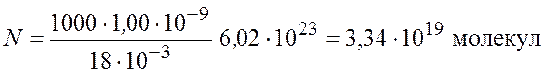 .
.
Массу одной молекулы ![]() можно
найти по формуле
можно
найти по формуле
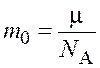 .
.
Подставив значения ![]() и
и ![]() , найдем массу молекулы воды
, найдем массу молекулы воды
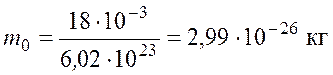 .
.
Если молекулы воды плотно прилегают друг к другу, то можно
считать, что на каждую молекулу приходится объем (кубическая ячейка) ![]() . Отсюда
. Отсюда
![]() . (8.1)
. (8.1)
Объем одной молекулы ![]() найдем,
разделив молярный объем
найдем,
разделив молярный объем ![]() на число молекул в
моле, т. е. на число Авогадро
на число молекул в
моле, т. е. на число Авогадро ![]() ,
,
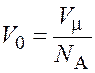 .
(8.2)
.
(8.2)
Молярный объем (объем одного моля вещества) можно найти одним из двух следующих способов:
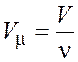 ;
; 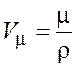 .
(8.3)
.
(8.3)
Подставив выражение (8.2) и второе из (8.3) в формулу (8.1), получим
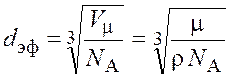 .
.
Произведем вычисления
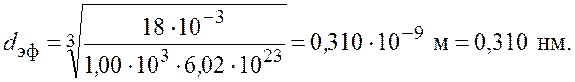
Ответ: ![]()
![]()
![]()
1. Микроскопическая пылинка
углерода ![]() обладает массой 0,175 нг. Найти
количество вещества
обладает массой 0,175 нг. Найти
количество вещества ![]() и число атомов
и число атомов ![]() в пылинке.
в пылинке.
2. Газ при температуре 364
К и давлении 785 кПа имеет плотность 5,25 ![]() Найти
массу одной молекулы газа.
Найти
массу одной молекулы газа.
3. В сосуде объемом 3,75 л находится 0,525 моль идеального газа. Найти концентрацию молекул в сосуде.
4. Найти среднее расстояние
между центрами молекул азота ![]() при нормальных
условиях.
при нормальных
условиях.
5. Первоначально идеальный газ занимал объем 12,42 л. При изобарном охлаждении на 40,0 К объем газа стал равным 10,62 л. Найти начальную температуру газа.
6. Идеальный газ массой 6,30 г занимает объем 4,00 л при температуре 280 К. После изобарного нагревания газа его плотность стала равной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.