Модель строения атома водорода по теории Бора: Учебно-методическое обеспечение практического занятия

5.3. Модель строения атома водорода по теории Бора (2 часа)

5.3.1. Учебная цель занятия

Научить студентов применять следующие понятия и законы:Планетарная модель атома. Модель строения атома водорода по теории Бора.

5.3.2. Методические указания к проведению занятия

Для решения задач используется теория Бора для водородоподобных атомов. При ее изменении необходимо указать ее недочеты, подчеркнув, что слабой стороной теории ее внутренняя логическая противоречивость: она не была последовательно классической, ни последовательно квантовой теорией. Указать на связь главного квантового числа n с энергией и радиусом орбит электрона в водородоподобном атоме. Зная величину полной энергии атома, вычислить кинетическую, потенциальную энергии, скорость, период вращения электрона при его движении по орбите.

В конце решения задач необходимо сформулировать принцип соответствия Бора.

5.3.3. Рекомендуемая литература

[4], Т4, 3.1–3.7[4];  [8] стр. 9-13.

5.3.4. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

Пример 1.  Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить в электронвольтах энергию испущенного при этом фотона.

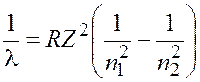                                    ,                                    (1.1)

где  – длина волны фотона;  – постоянная Ридберга;  – заряд ядра в относительных единицах (при  формула переходит в сериальную формулу для водорода);  – номер орбиты, на которую перешел электрон;  – номер орбиты, с которой перешел электрон ( и  – главные квантовые числа).

Энергия фотона связана с длиной волны излучения известным соотношением

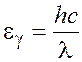                                              .                                              (1.2)

С учетом выражения (14.1) формула (14.2) может быть переписана в виде

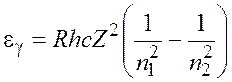                                 .                                  (1.3)

Так как величина  есть энергия ионизации  атома водорода, то для упрощения расчетов сделаем замену и перепишем выражение (1.3):

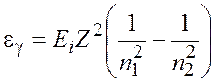                                   .                                   (1.4)

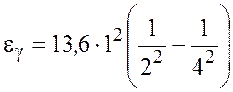Вычисления по формуле (1.4) выполним во внесистемных единицах, зная, что  эВ; :

                      эВ  эВ.

Ответ:  эВ.

Пример 2.  Оценить промежуток времени, за который электрон, движущийся вокруг ядра атома водорода по окружности радиусом  м, упал бы на ядро из-за потери энергии на излучение. 

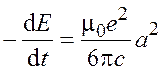                                       ,                                        (2.1)

где  – магнитная постоянная;  – заряд частицы;  – скорость света в вакууме;  – ускорение частицы.

В атоме водорода электрон движется под действием силы Кулона, поэтому в соответствии со вторым закон Ньютона

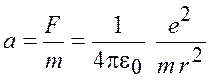                                   ,                                    (2.2)

где  – электрическая постоянная;  – радиус орбиты.

Подставим (2.2) в (2.1) и получим

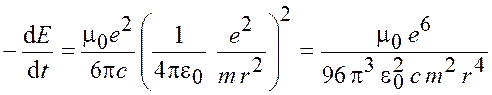            .            (2.3)

Кинетическая энергия электрона

                                          .

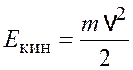Воспользуемся еще раз вторым закон Ньютона:

                                              .

Несмотря на излучение, при приближенном вычислении ускорения можно пользоваться следующей формулой:

                                              .

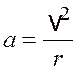Учитывая, что на электрон действует только сила Кулона, получим

                                     ,

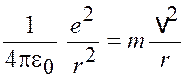откуда

                                       .

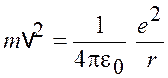Таким образом, кинетическая энергия электрона

                                      .

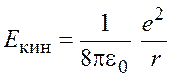Потенциальная энергия электрона

                                     .

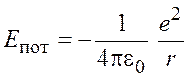Полная энергия электрона

        .

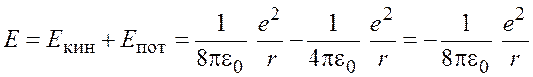Найдем изменение полной энергии во времени:

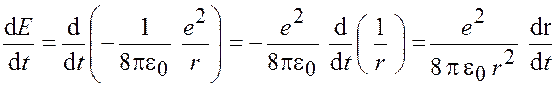      .       (2.4)

Выражение (2.4) подставим в левую часть формулы (2.3):

                        ;

                                 ;

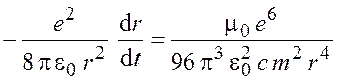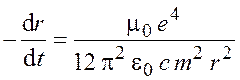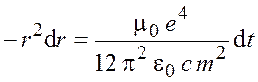                               .                                (2.5)

Проинтегрируем левую часть выражения (2.5) от  до 0, правую – от 0 до :

       ;       ;

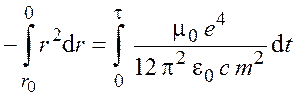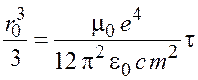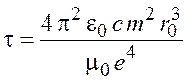                                     .                                     (2.6)

Произведем вычисления по формуле (2.6):

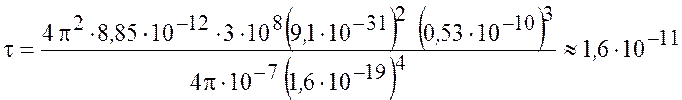 с.

Ответ:  с.

Пример 3.  Покоившийся атом водорода испустил фотон, соответствующий головной линии серии Лаймана. Найти скорость отдачи, которую получил атом, и отношение кинетической энергии атома к энергии испущенного фотона.