Физика \ Физика

Теплоёмкость твёрдых тел: Учебно-методическое обеспечение практических занятий

Страницы работы

17 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

6.7. теплоёмкость твёрдых тел (4 часа)

6.7.1. Учебная цель занятия

Показать студентам, что классическая теория теплоёмкости имеет ряд недостатков, которые в первую очередь проявляются в области низких и криогенных температур. Это относится ко всем веществам независимо от их агрегатного состояния. Научить студентов пользоваться квантовой теорией теплоёмкости для нахождения расчётных значений теплоёмкости при различных температурах. Показать, что лишь в области умеренных температур классическая теория теплоёмкости даёт те же результаты, что и квантовая теория.

6.7.2. Методические указания к проведению занятий

6.7.3. Рекомендуемая литература

[2] §2.1-2.8; 5.1-5.12 [6] стр. 271-277.

6.7.4. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Найти среднюю кинетическую энергию вращательного движения одной молекулы кислорода при температуре , а также кинетическую энергию вращательного движения всех молекул кислорода массой .

Дано:

Решение

;

– ?

Двухатомная молекула кислорода обладает двумя степенями свободы вращательного движения: . Поэтому в соответствии с законом Больцмана о равномерном распределении энергии по степеням свободы средняя энергия вращательного движения

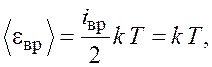(1.1)

где – постоянная Больцмана; – термодинамическая температура газа.

Кинетическая энергия вращательного движения всех молекул газа

(1.2)

Число всех молекул газа

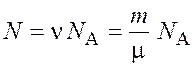, (1.3)

где – количество вещества; – постоянная Авогадро.

Подставив выражение (1.3) в формулу (1.2), получаем

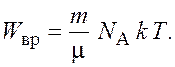(1.4)

Произведем вычисления

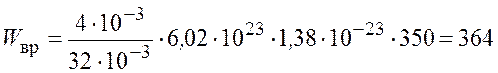Дж;

Дж.

Ответ: Дж, Дж.

Пример 2. Найти концентрацию молекул одноатомного идеального газа в сосуде объемом 2,00 л при температуре 27 °С, если его внутренняя энергия равна 300 Дж.

Дано:

Решение

= 2,00 л = ;

= 27 °С, Т = 300 К;

= 300 Дж.

– ?

Концентрация молекул

где N – число молекул в объеме V.

Внутренняя энергия газа определяется как сумма кинетических энергий всех молекул газа. Для одноатомного идеального газа

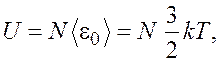
откуда число молекул

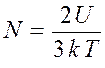Подставив полученное выражение для числа молекул газа в формулу для концентрации, получим

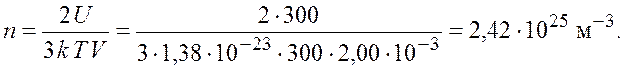
Ответ:

Пример 3. Вычислить удельную теплоемкость при постоянном объеме и при постоянном давлении неона и водорода , принимая эти газы за идеальные.

Дано:

Решение

;

– ?

Удельные теплоемкости идеальных газов выражаются формулами:

;

где – число степеней свободы молекулы газа; – молярная масса.

Произведем вычисления:

– для неона

;

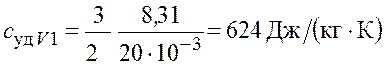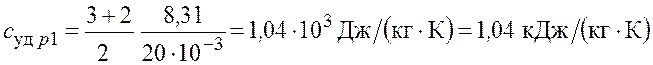– для водорода

;

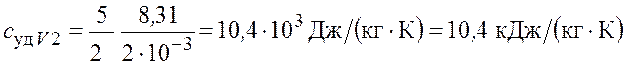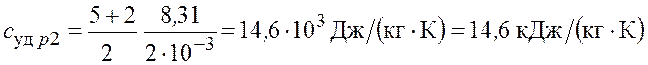Ответ: ; ;

; .

Пример 4. Вычислить удельные теплоемкости при постоянном объеме и при постоянном давлении смеси неона и водорода , если массовые доли неона и водорода составляют и . Значения удельных теплоемкостей взять из предыдущего примера.

Дано:

Решение

;

– ?

Удельную теплоемкость смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на выразим двумя способами

(4.1)

(4.2)

где – удельная теплоемкость неона; – удельная теплоемкость водорода.

Приравняв правые части выражений (4.1) и (4.2) и разделив обе части полученного равенства на получим

откуда

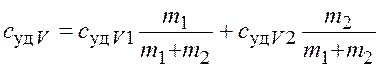, (4.3)

или

, (4.4)

где и – массовые дол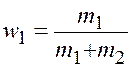и, и .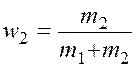

Рассуждая так же, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении

. (4.5)

Произведем вычисления по формулам (4.4) и (4.5)

;

Ответ: , .

Пример 5. Раствор состоит из двух массовых частей воды и одной массовой части этилового спирта. Определить удельную теплоемкость раствора. Удельная теплоемкость воды равна , этилового спирта – .

Дано:

Решение

;

– ?

Для нагревания воды, спирта и смеси на необходимы следующие количества теплоты:

(5.1)

(5.2)

(5.3)

где , , – удельные теплоемкости.

Из закона сохранения энергии следует, что

. (5.4)

Подставим формулы (5.1) – (5.3) в закон (5.4) и получим

откуда, с учетом ,

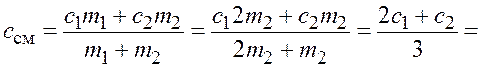
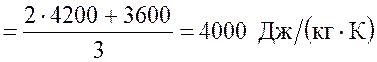Ответ: .

Пример 6. В калориметр, содержащий 2,00 кг воды температурой 15 °С, положили 1,00 кг льда температурой минус 20 °С. Какая температура установилась в калориметре? Каким оказалось содержимое калориметра после установления в нем теплового равновесия? Удельная теплоемкость льда – , воды – , удельная теплота плавления льда – . Теплоемкость калориметра не учитывать.

Дано:

Решение

= 2,00 кг;

;

= 1,00 кг;

;

– ?

Будем искать температуру смеси , считая, что весь лед расплавится. Тогда, за счет охлаждения воды, находящейся в калориметре, лед должен нагреваться до температуры плавления льда , затем расплавиться, а образовавшаяся при плавлении вода массой должна нагреваться до температуры .

Теплота нагревания льда

Теплота плавления льда

Теплота нагревания воды, образовавшейся изо льда,

Теплота, полученная при охлаждении воды массой ,

Составим уравнение теплового баланса

;

откуда температура смеси

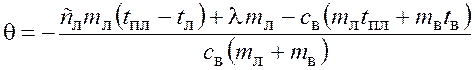Рассчитаем температуру смеси

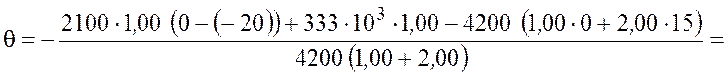
Итак, получилось, что при плавлении всего льда температура в калориметре должна была бы понизиться до минус 19,7 °С. Однако минимальная температура воды не может быть меньше температуры плавления . Отсюда следует, что лед расплавится лишь частично, а температура в калориметре установится = 0 °С.

Следовательно, за счет охлаждения воды в калориметре до лед нагревается до и часть его расплавится.

Теплота нагревания льда

Теплота плавления льда массой

Теплота, полученная при охлаждении воды массой ,

Составим уравнение теплового баланса

;

откуда масса расплавленного льда

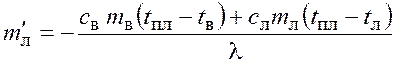Рассчитаем массу расплавленного льда

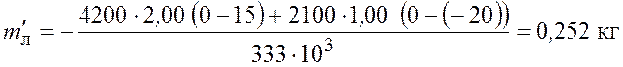Таким образом, в калориметре после установления теплового равновесия будет лед в количестве

и вода в количестве

Ответ: = 0 °С; = 2,252 кг; = 0,748 кг.

Пример 7. Идеальный газ находится под поршнем в вертикально расположенном цилиндре объемом 10,0 л. Температура газа 900 К, площадь поршня , масса 10,0 кг. На сколько градусов увеличили температуру газа, если работа расширения оказалась равной 50,0 Дж? Поршень перемещается без трения. Атмосферное давление 101 кПа.

Дано:

Решение

= 10,0 л = ;

= 900 К;

= 50,0 см² = ;

= 10,0 кг;

= 50,0 Дж;

Па.

– ?

Давление, под которым находится газ, складывается из давления атмосферы и давления, создаваемого за счет веса поршня,

. (7.1)

Поскольку поршень перемещается без трения, то по мере расширения газа он будет перемещаться

вверх и давление будет оставаться неизменным, т. е. процесс будет изобарным.

Работа идеального газа в изобарном процессе

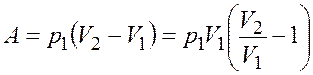. (7.2)

Отношение объемов найдем из уравнения изобарного процесса (закон Гей-Люсака)

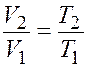. (7.3)

Подставив выражение (27.3) в формулу (27.2), получим

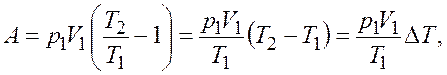
откуда с учетом соотношения (27.1)

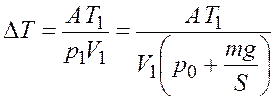Произведем вычисления

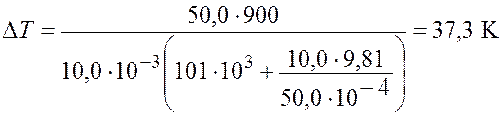Ответ: = 37,3 К.

Пример 8. В цилиндре под поршнем находится водород массой при температуре Водород сначала расширился адиабатно, увеличив свой объем в раз, а затем был сжат изотермически, причем объем газа уменьшился в раз. Найти температуру в конце адиабатного расширения и работу, совершенную газом при этих процессах. Изобразить процесс графически.

Дано:

Решение

;

– ?

Графическое изображение процессов дано на рис. 8.1.

Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением

, (8.1)

где – коэффициент Пуассона (показатель адиабаты)

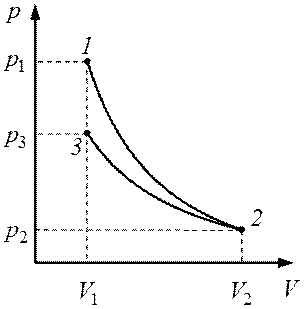
Рис. 8.1

Для двухатомной молекулы водорода , поэтому .

Из соотношения (8.1) получаем следующее выражение для конечной температуры:

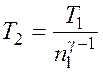Работа газа при адиабатном расширении может быть определена по формуле

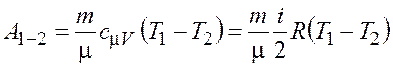Работа газа при изотермическом процессе может быть выражена в виде

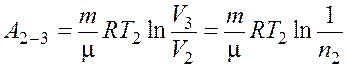Произведем вычисления

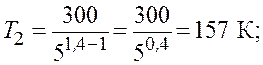
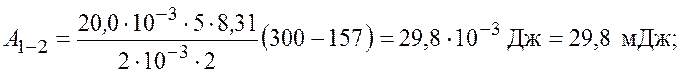
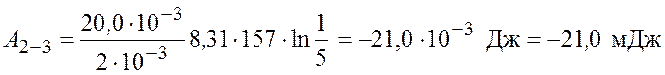Отрицательное значение работы означает, что при сжатии работа над газом совершается внешними силами.

Ответ: ,

Пример 9. Кислород массой занимает объем и находится под давлением . Газ был нагрет сначала при постоянном давлении до объема а затем при постоянном объеме до давления Найти изменение внутренней энергии газа, совершенную им работу и теплоту , переданную газу. Построить график процесса.