Основные законы магнитного поля: Учебно-методическое обеспечение практического занятия

3.5. Основные законы магнитного поля (2 часа)

3.5.1. Учебная цель занятия

Научить студентов применять следующие понятия и законы:Индукция магнитного поля, напряженность магнитного поля. Силовые линии магнитного поля. Принцип суперпозиции магнитных полей. Закон Био-Савара-Лапласа. Закон полного тока.

3.5.2. Методические указания к проведению
занятия

В качестве основной характеристики магнитного поля следует вводить магнитную индукцию, основываясь на силовом действии магнитного поля. Расчет индукции производить либо на основании закона Био-Савара-Лапласа и принципа суперпозиции, либо с помощью закона полного тока. Показать, что закон Био-Савара-Лапласа, а следовательно, и формулы выведенные с его помощью, справедливы только для линейных токов, т. е. проводников у которых не учитываются их магнитные свойства. В тех случаях, когда конфигурация токов, создающих поле, достаточно симметрична, для нахождения магнитной индукции используется закон полного тока. При решении задач, если студенты не знают выражения для индукции простейших полей: поле прямого тока, бесконечно длинного и конечной длины, поле на оси витка, необходимо сделать вывод этих формул.

Задачи, посвященные действию магнитного поля на проводники с током, включают расчет силы Ампера, действующей со стороны магнитного поля на линейные токи.

Рассматривая движение заряженных частиц в магнитном поле по окружности, используя второй закон Ньютона определить центростремительное ускорение, радиус окружности и период обращения частицы. Рассмотреть случай, когда скорость частицы образует с направлением однородного магнитного поля угол , отличный от нуля и . В каждом конкретном случае, решение задач сопровождать построением траектории движения частицы.

3.5.3. Рекомендуемая литература

[3] 5.1- 5.3;  [7] §3.

3.5.4. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

Пример 1. По двум бесконечно длинным параллельным проводникам текут токи одного направления силой 10,0 А. Вычислить индукцию магнитного поля в точке, которая расположена на расстоянии 40,0 см от одного проводника и 30,0 см от другого, если расстояние между проводниками 50,0 см.

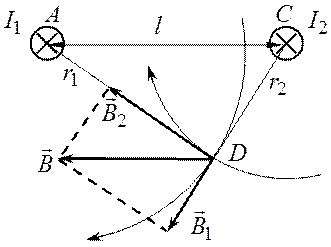
Рис. 1.1

Направление магнитных силовых линий связано правилом правого винта с направлением токов. Касательные к силовым линиям в точке D дают направление векторов  и . Из соотношения размеров , ,  видно, что треугольник AСD прямоугольный.

Так как вектор  перпендикулярен AD, а вектор  перпендикулярен СD, то угол между векторами  и  прямой. Поэтому искомая индукция

                                          ;

                                       .                                        (1.1)

Модули векторов  и  находим для прямых бесконечных проводников:

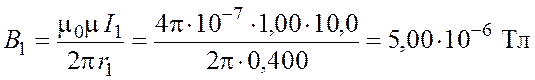        ;        (1.2)

         .

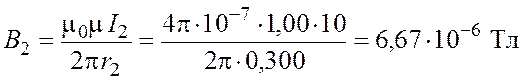Индукцию в точке D находим по формуле (1.1):

.

Ответ: .

Пример 2. По проводу, согнутому в виде равностороннего треугольника со стороной  мм, течет ток силой  А. Найти индукцию  в точке М, лежащей на продолжении одной из сторон треугольника на расстоянии  мм от ближайшей вершины.

Согласно принципу суперпозиции магнитных полей,

                              ,

где , ,  – магнитные индукции, создаваемые в точке  соответствующими сторонами треугольника ,  и .

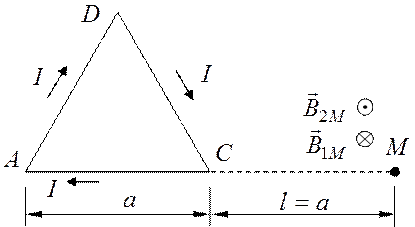Рис. 2.1

Найдем направления векторов ,  и .

По правилу правого винта вектор  направлен перпендикулярно плоскости чертежа «от нас», а вектор  – «к нам».

Для нахождения  обратимся непосредственно к закону Био–Савара–Лапласа:

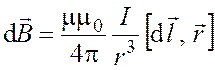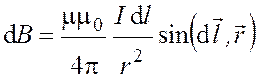        ,          ,        (2.1)

где  – электрический ток;  – элемент длины провода; вектор  совпадает по направлению с током ; – радиус-вектор, проведенный от элемента  к точке наблюдения.

Применяя соотношение (2.1) к любому элементу длины  стороны  треугольника, можно увидеть, что угол между  и радиусом-вектором , проведенным из  в точку , составляет , следовательно, . Так как это справедливо для любого элемента проводника АС, то

                                             .

Следовательно, величина результирующего поля (направление вектора  принято за положительное)

                                     .                                     (2.2)

Найдем модули векторов  и .

Стороны треугольника представляют собой проводники конечной длины, поэтому модули этих векторов найдем по формуле

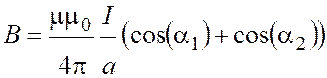                         ,                          (2.3)

где    – расстояние  от  точки  наблюдения  до  оси  проводника;  – угол между проводником и радиусом-вектором, проведенным из начала