Явление электромагнитной индукции: Учебно-методическое обеспечение практического занятия

3.8. Явление электромагнитной индукции (2 часа)

3.8.1. Учебная цель занятия

Научить студентов применять следующие понятия и законы: Магнитный поток. Явление электромагнитной индукции. Закон Фарадея. Правило Ленца. Индуктивность. Явление самоиндукции. Энергия однородного магнитного поля. Энергия проводника с током. Объемная плотность энергии магнитного поля.

3.8.2. Методические указания к проведению
занятия

Анализ задач по данной теме начинается с выяснения причин, вызывающих изменение магнитного потока, причин возникновения направленного движения зарядов или их перераспределения. Это позволяет найти направление индукционного тока или знак э.д.с. индукции с помощью правила Ленца. При этом подчеркивается, что электродвижущая сила и ток индукции независимо от причин, вызывающих их появление находятся по формулам: , .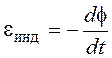

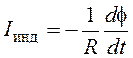Далее выясняется, в каком проводнике возникает э.д.с. индукции. Если дан замкнутый проводник (контур), поток сквозь которого изменяется, то его целесообразно выразить как функцию времени. Тогда э.д.с. или ток индукции находятся дифференцированием функции, при этом ток или знак э.д.с. зависят от знака производной . Если в магнитном поле движется отдельный проводник, а не контур в целом, то при использовании приведенных формул под  следует понимать абсолютное значение магнитного потока, пересеченного проводником за время  его движения; знак э.д.с. определяется независимо от расчета.

Явление самоиндукции рассматривается как частный случай явления электромагнитной индукции. При анализе задач осмысливается вся совокупность явлений, возникающих в электрических цепях при изменении силы тока. Обратить внимание на то, что индуктивность зависит от геометрии проводника, магнитных свойств среды и не зависит от силы тока только при отсутствии ферромагнетиков.

3.8.3. Рекомендуемая литература

[3] 6.1-6.7; [7] §3.

3.8.4. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

Пример 1. В однородном магнитном поле с индукцией  мТл равномерно с частотой  вращается металлический стержень длиной  м. Ось вращения О (рис. 1.1), проходящая через один из концов стержня, перпендикулярна стержню и параллельна линиям индукции магнитного поля. Найти разность потенциалов, возникающую на концах стержня, и определить ее знак.

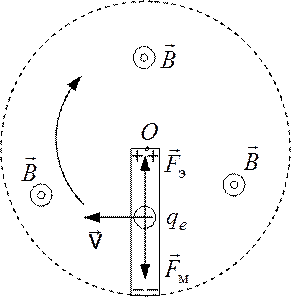Рис. 1.1

1-й  способ.

Разность потенциалов на концах стержня в рассматриваемом случае совпадает с ЭДС индукции:

                                            .

Для нахождения ЭДС, возникающей на концах стержня, воспользуемся формулой

                                           .

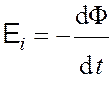Под потоком  будем понимать поток вектора индукции, пронизывающий площадь, зачерчиваемую стержнем при вращении:

                                   .

Так как вектор  перпендикулярен плоскости вращения стержня, то , поэтому магнитный поток .

За один оборот стержень зачерчивает площадь , а за время

                                   .

Магнитный поток, пересекаемый стержнем за время ,

                                .

Окончательно для величины ЭДС получаем

                               .

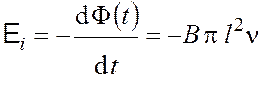Разность потенциалов на концах стержня

                                   .

2-й  способ.

При движении стержня вместе с ним с такой же скоростью перемещаются свободные носители заряда в проводнике – электроны. Со стороны поля  на каждый электрон начнет действовать магнитная составляющая силы Лоренца , направленная вдоль стержня. Под действием этой силы электроны будут смещаться к одному из концов стержня. Вследствие этого смещения на одном конце будет накапливаться отрицательный заряд, а на другом появится положительный заряд. Эти заряды создают электрическое поле , которое будет действовать на электроны с силой . Эта сила всегда направлена противоположно силе . С увеличением количества электронов на одном из концов стержня будет увеличиваться поле  и, следовательно, сила . Движение электронов вдоль стержня будет продолжаться до тех пор, пока сила  не станет равной силе . После этого перераспределение электронов прекратится и разность потенциалов вдоль стержня будет оставаться постоянной до тех пор пока не изменится или частота вращения, или магнитное поле.

Этот способ позволяет определить знак потенциала. В случае, показанном на рис. 1.1 на удаленном от оси вращения конце стержня будет отрицательный потенциал.

Получим формулу для разности потенциалов.

                                             ;

                                          ;

                                              .

Связь напряженности и потенциала электрического поля вдоль стержня

                                            .

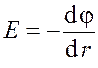Связь линейной и угловой скоростей

                                               .

Из трех последний формул получим

                                          ;

                                        .

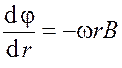Проинтегрируем последнее выражение

                                     ;

                                     .

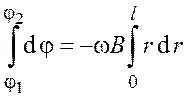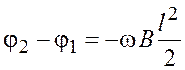Связь угловой скорости и частоты вращения