Явление электромагнитной индукции: Учебно-методическое обеспечение практического занятия, страница 2

                                             .

Разность потенциалов на концах стержня

                                 .

Произведем вычисления:

               В.

Ответ:  В.

Пример 2. Прямоугольная рамка вращается  в однородном магнитном поле с частотой  с^–1. Ось вращения лежит в плоскости рамки и перпендикулярна силовым линиям. В момент  скорость вращения начинает уменьшаться с ускорением  рад/с. Площадь рамки  см². Рамка содержит  витков тонкого провода. Индукция магнитного поля равна  мкТл. Найти ЭДС индукции в момент  с, если в момент  вектор индукции был перпендикулярен плоскости рамки.

Дано:	Решение
с–1;  рад/с;  см2 м2;  витков;  мкТл Тл; °;  с.  –?	Мгновенное значение ЭДС индукции в проводящем контуре определим по закону Фарадея–Ленца: , где  – потокосцепление рамки. Так как через все витки рамки проходит один и тот же магнитный поток, то потокосцепление рамки

                                            ,

где  – число витков;  – магнитный поток через один виток,

                                       ,

здесь  – угол между нормалью к поверхности рамки и вектором .

При равнозамедленном вращении угол  изменяется по закону

                                   ,

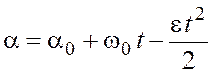где  – угловая скорость, .

Таким образом, потокосцепление рамки зависит от времени по закону

     .

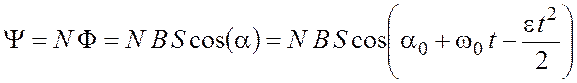Найдем ЭДС индукции:

.

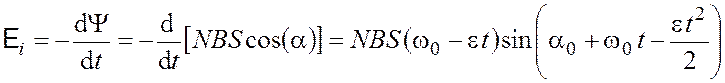Выразим  через  и окончательно получим

           .

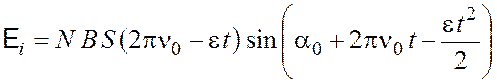Произведем вычисления:

    

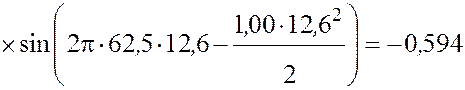             В.

Ответ:  В.

Пример 3. Две параллельные медные шины, расположенные в горизонтальной плоскости, помещены в однородное вертикальное магнитное поле с индукцией  мТл. Шины с одного конца замкнуты на сопротивление  Ом. По шинам под действием постоянной силы со скоростью  м/с скользит проводящая перемычка, перпендикулярная шинам. Найти величину силы, если расстояние между шинами (длина перемычки)  м; трением пренебречь.

Дано:	Решение
Ом;  м/с;  м. ?	При движении перемычки меняется площадь контура  (рис. 35.1), а следовательно, и поток через него.

Рис. 3.1

В результате этого в контуре возникают ЭДС индукции и индукционный ток, причем, согласно правилу Ленца, направление индукционного тока должно быть таким, чтобы он препятствовал изменению магнитного потока через контур. Направление индукционного тока показано на рис. 3.1. Положительную нормаль направим так, чтобы она была связана с направлением индукционного тока правилом правого винта. Таким образом, сила Ампера, действующая на движущуюся перемычку, должна быть направлена в сторону, противоположную скорости  и силе .

Найдем, зависимость магнитного потока через контур  от времени

         ,

где  – расстояние  от  замкнутого  конца  шин  до перемычки;  – расстояние от замкнутого конца шин до перемычки в момент времени ; , т. к. угол между  и  равен 180°.

Получим выражение для ЭДС индукции и индукционного тока

               ;              .

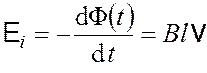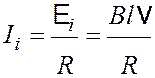Найдем силу Ампера, действующую на перемычку,

                                   .

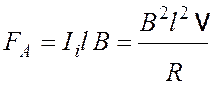Записав второй закон Ньютона в проекции на направление движения, получаем искомую силу :

                           ,          .

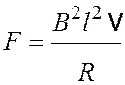Произведем вычисления

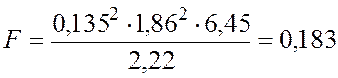                       Н.

Ответ:  Н.

3.8.5. Задачи для решения на практических
занятиях

1. В однородном магнитном поле, индукция которого  мТл, равномерно с круговой частотой  рад/с вращается рамка, содержащая  витков провода. Площадь рамки  см². Ось вращения находится в плоскости рамки и составляет угол  с направлением магнитного поля. Найти максимальное значение ЭДС индукции в рамке.

2. В однородном магнитном поле с индукцией  Тл вращается квадратная рамка со стороной  см, состоящая из  витков медного провода сечением  мм². Максимальное значение силы тока в рамке  мА. Определить число оборотов рамки в секунду, если удельное сопротивление меди  Ом·м.

3. В однородном магнитном поле, индукция которого  мТл, равномерно с частотой  с^–1 вращается на непроводящей нити металлический стержень, привязанный к нити за один из своих концов. Длина нити  мм, длина стержня  мм. Найти разность потенциалов, возникающую на концах стержня, если линии магнитной индукции перпендикулярны плоскости вращения нити и стержня.

4. Через катушку индуктивностью  мГн протекает ток, изменяющийся по закону  А. Определить закон изменения ЭДС самоиндукции и максимальное значение ЭДС самоиндукции.

5. Чему равен коэффициент самоиндукции катушки с железным сердечником, если за время  с ток в цепи изменился с  А до  А, а наведенная при этом ЭДС на концах катушки  В?

3.8.6. Номера задач для самостоятельной работы студентов

3.8.2; 3.8.6; 3.8.11; 3.8.15; 3.8.23; 3.8.25; 3.8.39; 3.9.4; 3.9.7; 3.9.12; 3.9.26; 3.9.30. [7]