Напряженность электростатического поля. Принцип суперпозиции. Теорема гаусса: Учебно-методическое обеспечение практического занятия

заданной конфигурации электрических зарядов. Рассматриваемые поля (в вакууме) создаются электрическими зарядами, находящимися на телах, физическая природа которых не учитывается. Распределение зарядов на таких телах задается условием задачи.

Используемые методы расчета – принцип суперпозиции полей и теорема Гаусса, записанная в интегральной форме.

При достаточно симметричной конфигурации зарядов, используя теорему Гаусса, найти напряженность результирующего поля как функцию координат.

3.1.3. Рекомендуемая литература

[3] 3.1, 3.2, 3.3;  [7] §1.

3.1.4. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

Пример 1. Три точечных заряда по  нКл расположены в вершинах равностороннего треугольника. Какой заряд  нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в состоянии механического равновесия?

Дано:	Решение
– ?	Все три заряда, расположенные в вершинах треугольника, находятся в одинаковых условиях. Поэтому достаточно рассмотреть один из зарядов, например . На рис. 1.1 показаны силы, действующие на этот заряд.

 

Рис. 1.1

Выясним, какой заряд  необходимо поместить в центр треугольника, чтобы заряд  находился в механическом равновесии. Условием такого равновесия является равенство нулю векторной суммы всех действующих на заряд  сил:

                                      ;

                                           ,                                           (1.1)

где , ,  – силы, с которыми на заряд  действуют соответственно заряды ;  – равнодействующая сил  и .

Для нахождения равнодействующей силы  применим следствие из теоремы косинусов и тогда получим следующее выражение:

                          .                           (1.2)

В равностороннем треугольнике , расстояние от центра треугольника до его вершины определяется по формуле

                       .

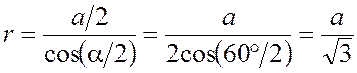Применив закон Кулона и имея в виду, что  найдем

                                    ,

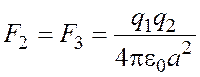откуда

     .

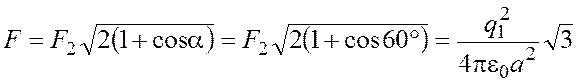С другой стороны, по закону Кулона

                                .

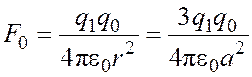Поскольку силы , а векторы сил  и  лежат на одной прямой и направлены в противоположные стороны, то из векторного равенства (1.1) можно получить скалярное:

                               ,          ;                               (1.3)

                                    ,

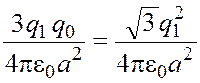откуда

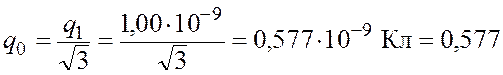 нКл.

Ответ:  нКл.

Пример 2. Два точечных заряда  Кл и  Кл находятся в керосине () на расстоянии 0,200 м друг от друга. Найти напряженность поля в точке, лежащей посередине между точечными зарядами, а также силу, действующую на электрон, помещенный в эту точку.

Дано:	Решение
Кл;  Кл;  м;  м; ;  Кл.  – ?  – ?	На рис. 2.1 показаны векторы напряженности полей, создаваемых двумя точечными зарядами. Рис. 2.1

Согласно принципу суперпозиции электрических полей, напряженность результирующего поля  может быть найдена как сумма векторов напряженности  и  полей, создаваемых отдельными зарядами:

                                          .                                          (2.1)

Так как векторы напряженности  и  направлены по одной прямой в противоположные стороны, то из векторного равенства (2.1) можно получить следующее скалярное:

                                          .                                          (2.2)

Напряженность поля точечного заряда выражается формулой

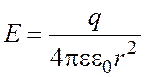                                         .                                         (2.3)

Подставляя в формулу (2.2) выражения для  и  и учитывая, что расстояния 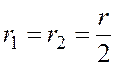, получим

     .

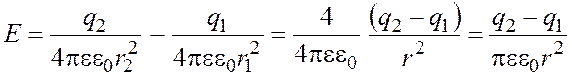Произведем вычисления:

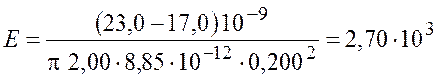             В/м.

Знак «плюс» показывает, что результирующее поле направлено в сторону вектора .

Сила, действующая на электрон, помещенный в эту точку,

          Н.

Знак «минус» показывает, что сила направлена противоположно вектору напряженности.

Ответ:  Н.

Пример 3. Два одинаковых положительных точечных заряда расположены на расстоянии  см друг от друга. Найти на прямой, перпендикулярной отрезку, соединяющему заряды и проходящей через его середину, точку, в которой напряженность электрического поля максимальна.

Дано:	Решение
см.  – ?	Изобразим на рис. 3.1 прямую , на которой должна лежать искомая точка.

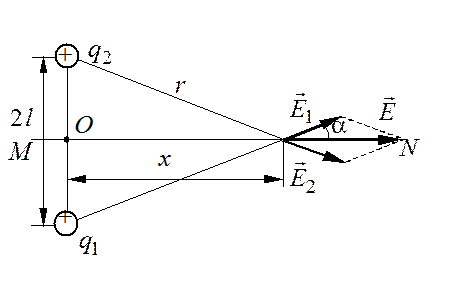
Рис. 3.1

Напряженность электрического поля в любой точке пространства может быть найдена согласно принципу суперпозиции

                                          .

При этом в точке , лежащей между зарядами, сумма векторов  и , одинаковых по модулю и противоположных по направлению, равна нулю. В точках прямой , весьма удаленных от зарядов, векторы  и  окажутся приблизительно одинаково направленными. Однако и в этом случае их равнодействующая близка к нулю, поскольку оба слагаемых быстро убывают при удалении от зарядов. Следовательно, на прямой  по обе стороны от зарядов должны быть точки, в которых напряженность поля достигает максимума.

Рассмотрим произвольную точку, расположенную на прямой  на расстоянии  от точки . Как видно из рисунка,

                                        ,                                        (3.1)

где  – угол между вектором  и осью .

Учитывая соотношения

                                          ;

                                     ,

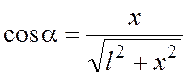вместо равенства (3.1), используя формулу напряженности поля точечного заряда, получим

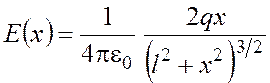                              .                               (3.2)

Чтобы найти максимум функции (3.2), продифференцируем ее по  и приравняем к нулю производную:

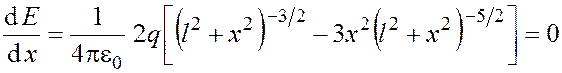.    (3.3)

Отсюда находим

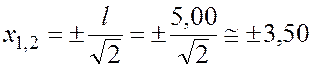                         см.

Два значения  соответствуют двум точкам, расположенным