Потенциал. Работа сил поля: Учебно-методическое обеспечение практического занятия

3.2. Потенциал. Работа сил поля (2 часа)

3.2.1. Учебная цель занятия

Научить студентов применять следующие понятия и законы: Принцип суперпозиции электростатических полей. Потенциал электростатического поля. Связь напряженности и потенциала. Работа сил электростатического поля по перемещению электрического заряда.

3.2.2.Методические указания к проведению занятия

В электростатике, а затем в электродинамике впервые в курсе физики рассматривается теория поля с использованием соответствующего математического аппарата. Задачи данного раздела и посвящены нахождению электростатического поля – расчету потенциала и напряженности – по заданной конфигурации электрических зарядов.

Используемые методы расчета – принцип суперпозиции полей и теорема Гаусса, записанная в интегральной форме.

Показать, что принцип суперпозиции позволяет найти потенциал как функцию координат, а затем используя формулы дифференциальной связи – напряженность поля. В тоже время в некоторых задачах целесообразно определять независимо друг от друга и потенциал, и напряженность методом суперпозиции, но при этом, не следует увлекаться расчетами сложных полей методом суперпозиции.

При достаточно симметричной конфигурации зарядов, используя теорему Гаусса, найти напряженность результирующего поля как функцию координат. Показать, что потенциал и разность потенциалов при этом рассчитываются с помощью формул интегральной связи напряженности и потенциала или разности потенциалов.

3.2.3. Рекомендуемая литература

[3] 3.1, 3.2, 3.3;  [7] §1.

3.2.4. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

Пример 1. Между двумя точечными зарядами 3,00 нКл и минус 1,00 нКл расстояние 10,0 см. На прямой, соединяющей заряды, найти положения точек относительно второго заряда, в которых электрический потенциал будет равен нулю.

На рис. 1.1 показано расположение зарядов  и  и знаки потенциалов поля  и , создаваемых указанными зарядами в точках D, K, L.

 

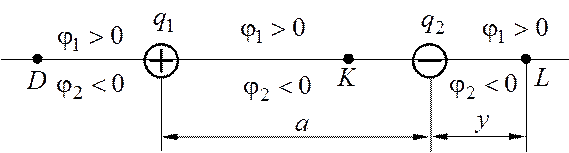Рис. 1.1

Потенциал является скалярной величиной, и его знак определяется знаком заряда, создающего поле. В соответствии с принципом суперпозиции потенциал поля будет равен нулю в той точке, где равна нулю алгебраическая сумма потенциалов.

Обозначим расстояние от второго заряда до точки L буквой «» (см. рис. 1.1). Найдем потенциалы  и  в точке L и приравняем их. Получаем линейное уравнение, корень которого даст координату точки L.

Потенциал поля, создаваемого первым зарядом в точке L,

                                     .

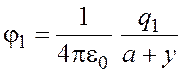Потенциал поля, создаваемого вторым зарядом в точке L,

                                        .

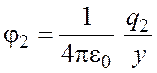Принцип суперпозиции для потенциала

                                          ,

или

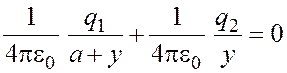                             .                             (1.1)

После подстановки в уравнение (1.1) числовых значений зарядов, с учетом их знаков и соответствующих преобразований, получим

                                     ,

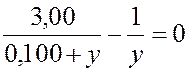откуда расстояние от второго заряда до точки L

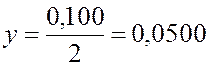                                   м.

Обозначим расстояние от второго заряда до точки K буквой «» (рис. 1.2). Найдем потенциалы  и  в точке K и приравняем их. Получаем линейное уравнение, корень которого даст координату точки K.

 

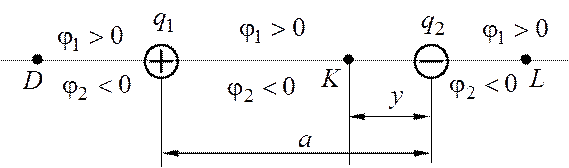Рис. 1.2

Потенциал поля, создаваемого первым зарядом в точке K,

                                     .

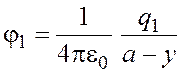Потенциал поля, создаваемого вторым зарядом в точке K,

                                       .

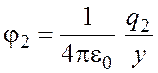Принцип суперпозиции для потенциала

                                          

или

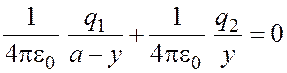                             .                             (1.2)

После подстановки в уравнение (1.2) числовых значений зарядов, с учетом их знаков и соответствующих преобразований, получим

                                     ,

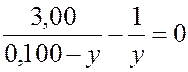откуда расстояние от второго заряда до точки K

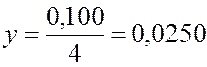                                   м.

Обозначим расстояние от второго заряда до точки D буквой «» (рис. 1.3). Найдем потенциалы  и  в точке D и приравняем их. Получаем линейное уравнение, корень которого даст координату точки D.

 

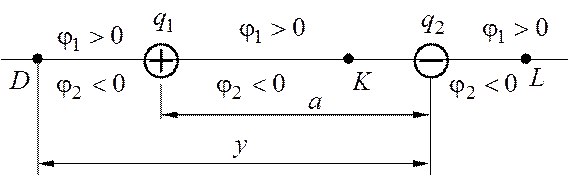Рис. 1.3

Потенциал поля, создаваемого первым зарядом в точке D,

                                     .

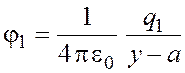Потенциал поля, создаваемого вторым зарядом в точке D,

                                       .

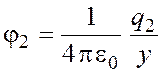Принцип суперпозиции для потенциала

,         или 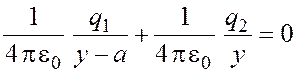        .     (1.3)

После подстановки в уравнение (1.3) числовых значений зарядов, с учетом их знаков и соответствующих преобразований, получим

                                     ,

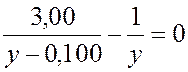откуда расстояние от второго заряда до точки D

                                        м.

Так как  это расстояние, а оно всегда положительное, то точка D не удовлетворяет условию задачи. Следовательно, потенциал поля равен нулю только в двух точках: L и K.

Ответ:  м;  м.

Пример 2. Найти силу взаимодействия между заземленной проводящей сферой радиусом 10,3 см и точечным зарядом 15,0 нКл, находящемся на расстоянии 52,7 см от центра сферы.

Рис. 2.1

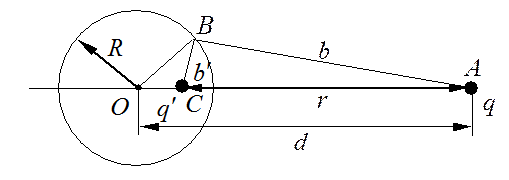Положение и величина фиктивных зарядов должны выбираться таким образом, чтобы одна из эквипотенциальных поверхностей поля (т. е. поверхность, в каждой точке которой потенциал одинаков), создаваемого