Алгоритмы цифровой фильтрации сигналов методом усреднения и исследование эффективности их работы, страница 5

 

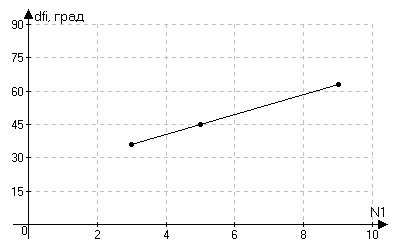
Рис. 4.2.7. Зависимость величины фазового сдвига от N₁.

 

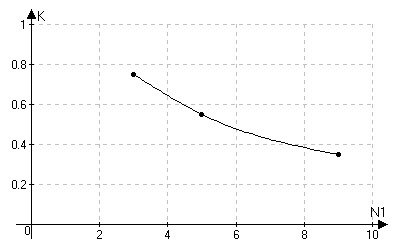
Рис.4.2.8. Зависимость К_Ф сдвига от N₁.

            Интересно отметить то, что с ростом величины корректирующего коэффициента

уменьшается коэффициент фильтрации. Это объясняется тем, что фильтр приближается

по своему характеру к фильтру с бесконечной памятью.

            Также отметим, что наблюдается фазовый сдвиг  выходного сигнала относительно

входного, что связано с наличием у фильтра памяти: влияние на результат предыдущих

значений больше, чем текущего, но при этом начиная с определенного момента влияние более ранних результатов скрадывается за счет их взаимокомпенсации.

Рассмотрим, как изменится результат при изменении периода дискретизации T_0.

Таблица 4.2.5. Параметры фильтра при различных значениях периода дискретизации

            (N₁ = 3, X₀ = 0, A = 1 В).

То есть для фильтра с постоянным коэффициентом коррекции уменьшение периода

дискретизации аналогично уменьшению N₁ приводит к росту реактивности системы.

            Исследуем реакцию фильтра на зашумленный сигнал.

  

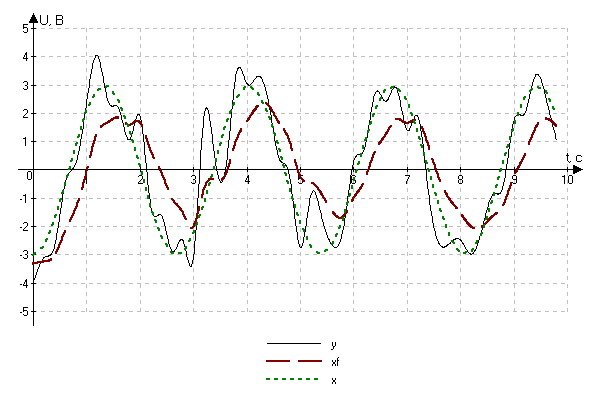
Рис. 4.2.9. Цифровая фильтрация сигнала при N₁ = 3, X₀ = -3.

            Теперь рассмотрим зависимость качества фильтрации при поданном на вход фильтра сигнале вида «белый шум».

Таблица 4.2.6. Параметры фильтра при различных значениях корректирующего коэффициента.