Алгоритмы цифровой фильтрации сигналов методом усреднения и исследование эффективности их работы, страница 2

( y – входной сигнал, xf – выходной сигнал фильтра).

В этом случае оценка эффективности фильтра:  Z = 1,0125

 

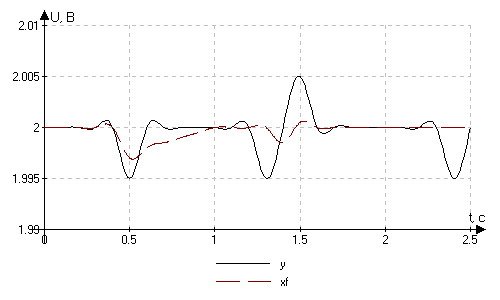
Рис. 4.1.2. Цифровая фильтрация сигнала при  X = 2 B.

Здесь Z = 1,0006.

            То есть в данном случае мы имеем дело с некой аддитивной помехой небольшой величины (до 0,005 В), что соответствует порядку величины погрешность ЦАП и АЦП (0,0025 В). Стоит отметить характер работы фильтра, который заключается в том, что со временем сигнал на его выходе стремится к заданному, то есть улучшается качество фильтрации помехи.

            Рассмотрим теперь реакцию фильтра на зашумленный постоянный входной сигнал.

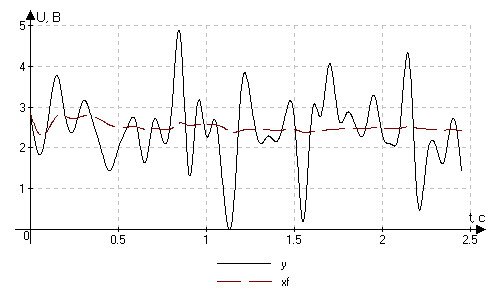
Рис. 4.1.3. Цифровая фильтрация сигнала при  X = 2,6 B (T₀ = 50 мс, N = 50).

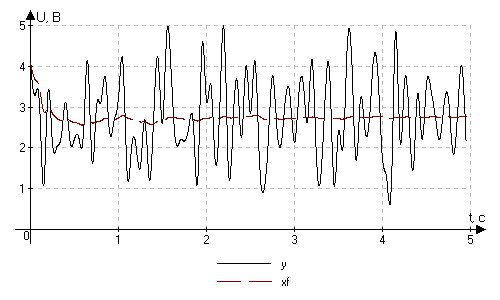
Рис. 4.1.4. Цифровая фильтрация сигнала при  X = 2,6 B (T₀ = 50 мс, N = 100).

            Отметим, что при наличии помехи все равно наблюдается приближение отфильтрованного сигнала к заданному уровню, причем, так как в его расчете используются все результаты, то качество отфильтрованного сигнала улучшается со временем, то есть с ростом числа замеров. Причина этого в том, что при большом объеме выборки снижается вес отдельного, возможно сильно отличающегося от среднего, результата.

            Далее рассмотрим работу фильтра при детерминированном динамическом сигнале на входе. В качестве такого сигнала возьмем синусоидальный сигнал. Сперва рассмотрим сигнал с нулевым средним значением.

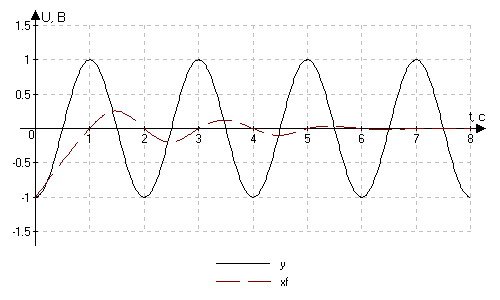
Рис. 4.1.5. Цифровая фильтрация сигнала при  X₀ = -1.

Рассмотрим, как влияет на результаты работы фильтра начальная величина сигнала

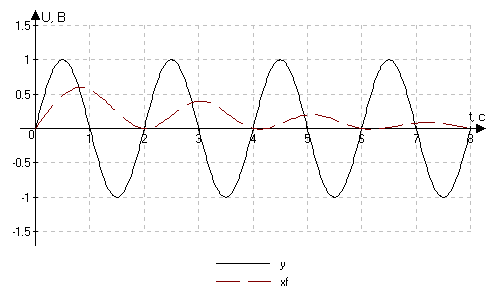
Рис. 4.1.6. Цифровая фильтрация сигнала при  X₀ = 0.

Рассмотрим, как изменится результат фильтрации, если исходный сигнал был подвергнут

воздействию белого шума.

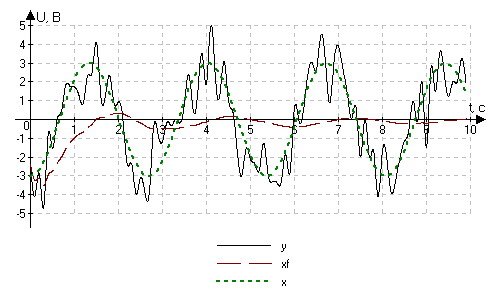
Рис. 4.1.7. Цифровая фильтрация сигнала при  X₀ = -3.

            По результатам исследований, приведенным выше, можно сказать, что фильтр

с бесконечной памятью не подходит для фильтрации динамических сигналов, поскольку

осуществляет усреднение по всей полученной выборке.

            Но стоит отметить, что на вид полученного на его выходе сигнала сказывается начальное значение сигнала. Переходные процессы выходного сигнала завершаются тем раньше, чем больше было начальное отклонение входного сигнала от среднего значения.

            Теперь рассмотрим реакцию фильтра на поданный на него сигнал вида «белый шум».

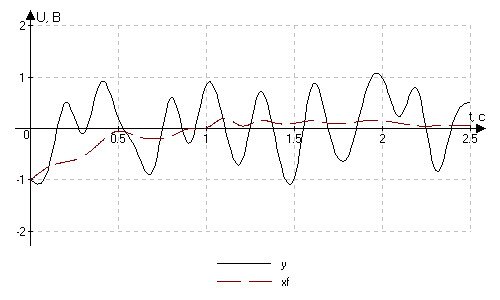
Рис. 4.1.8. Входной сигнал – «белый шум».

            Наличие «белого шума» на входе фильтра приводит к тому, что на выходе его имеем 0, что соответствует математическому ожиданию величины данного сигнала. Причем после того, как мы получим это значение, оно значительно не будет меняться и в бесконечности будет

равно нулю.

                         Таблица 4.1.1. Зависимость качества фильтрации от величины шума.