Алгоритмы цифровой фильтрации сигналов методом усреднения и исследование эффективности их работы, страница 3

            Таблица 4.1.2. Зависимость качества фильтрации от периода дискретизации.

 

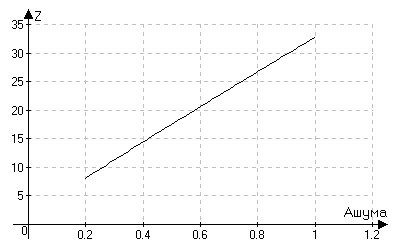
Рис. 4.1.9. Зависимость Z = f(α_шума).

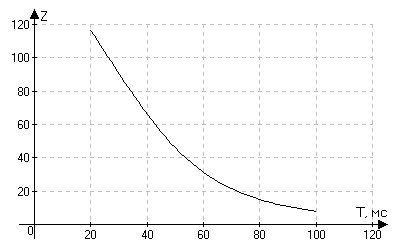
Рис. 4.1.10. Зависимость Z = f(T₀).

4.2. Рекуррентный алгоритм усреднения с постоянным коэффициентом коррекции

            Будем подавать на вход фильтра постоянный по величине входной сигнал Y = 1 В.

Исследуем зависимость выходного сигнала фильтра от величины корректирующего

коэффициента N₁.

  

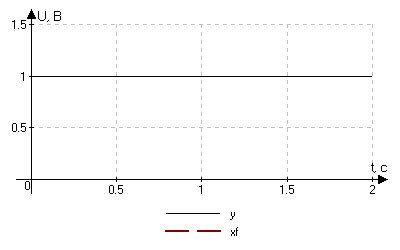
Рис. 4.2.1. Цифровая фильтрация сигнала при  N₁ = 2, X₀ = 0.

 

Рис. 4.2.2. Цифровая фильтрация сигнала при  N₁ = 4, X₀ = 0.

 

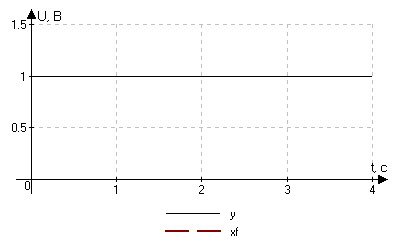
Рис. 4.2.3. Цифровая фильтрация сигнала при  N₁ = 9, X₀ = 0.

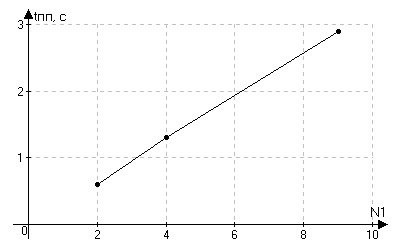
Таблица 4.2.1. Параметры фильтра при различных значениях корректирующего коэффициента.

            Отметим увеличение t_п.п. при увеличении N₁, что связано с большим влиянием

предыстории на результат.