Информатика и выч. техника \ ЭВМ и микропроцессорные системы

Задачі та вправи по дисципліні “ЕОМ і мікропроцесори” (з відповідями та розв’язками), страница 8

Подпись: a b c Y MSB LSB 0 0 0 0 0 0 0 0 1 0 1 1 0 1 0 0 1 0 0 1 1 1 0 1 1 0 0 0 0 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 0 0 Табл. 3 Введемо слідуючу систему кодування: 00 – всі канали справні; 11; 1,0; 01 – відмовив відповідно перший канал “a”; другий канал “b”; третій канал ”c”.

Тепер можна побудувати таблицю станів вузла.(Таб. 3)

З таблиці відомими засобами знаходимо:

  60.  На рис. 22 приведена схема включення перетворювача коду. Підсвітка кожного із елементів індикатора, утворюючих десяткові числа від 0 до 9 відбувається шляхом подачі одиничного сигналу на відповідний його вхід.

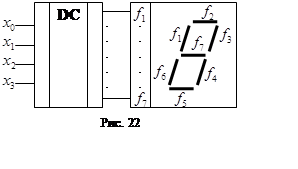Для побудови логічної схеми індикатора необхідно створити таблицю істиності логічних функцій перетворювача (див. табл. 4).

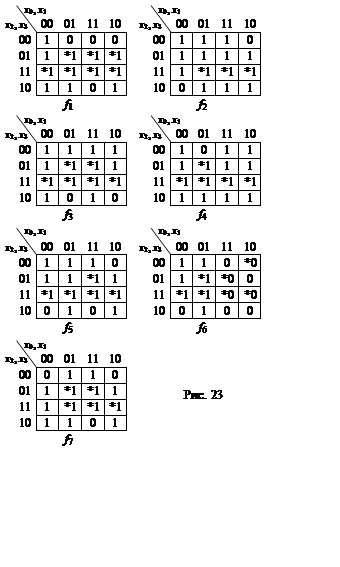
Специфіка таблиці 4 в тому, що частина значень двійково десяткового коду не визначена Це дозволяє спростити значення функцій f1-f7 Для мінімізації функцій f1-f7 представимо іх за допомогою карт Карно. (рис. 23).

Для мінімізації логічних функцій f1-f7 незаповнені клітини необхідно довизначити. Через те, що значення функцій відповідаючих цим клітинам для нас немають значення, ми можимо записати в ни як одиниці, так і нулі, виходячи лише із умови отримання мінімальної форми логічних функцій.

Довизначивши значення функцій в відповідності з рис. 23 після мінімізації маємо:

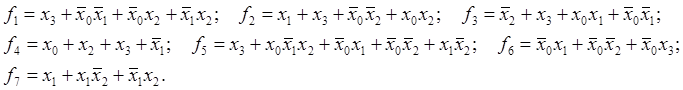
Реалізація цих функцій в вибраному базисі елементів відбувається за допомогою засобів, описаних в попередній задачі.

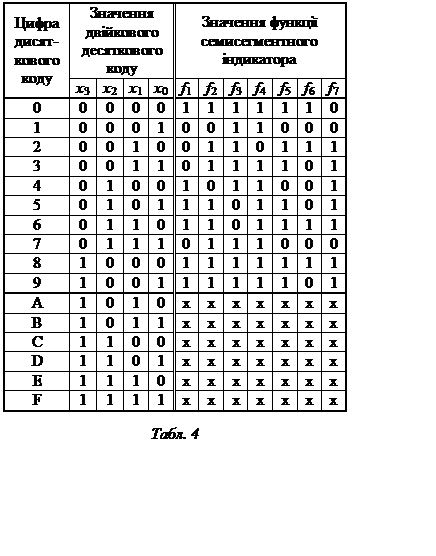
Подпись: Цифра дисят-кового коду Значення двійкового десяткового коду Значення функції семисегментного індикатора х3 х2 х1 х0 f1 f2 f3 f4 f5 f6 f7 0 0 0 0 0 1 1 1 1 1 1 0 1 0 0 0 1 0 0 1 1 0 0 0 2 0 0 1 0 0 1 1 0 1 1 1 3 0 0 1 1 0 1 1 1 1 0 1 4 0 1 0 0 1 0 1 1 0 0 1 5 0 1 0 1 1 1 0 1 1 0 1 6 0 1 1 0 1 1 0 1 1 1 1 7 0 1 1 1 0 1 1 1 0 0 0 8 1 0 0 0 1 1 1 1 1 1 1 9 1 0 0 1 1 1 1 1 1 0 1 А 1 0 1 0 х х х х х х х B 1 0 1 1 х х х х х х х C 1 1 0 0 х х х х х х х D 1 1 0 1 х х х х х х х E 1 1 1 0 х х х х х х х F 1 1 1 1 х х х х х х х Табл. 4

  61.  Код Грея називається одношаговим і його характерною особливістю є те, що при переході до наступної кодової комбінації змінюється тільки одна цифра. Його застосування дозволяє забезпечити високу точність перетворення різного роду механічних переміщень в цифровий код.

Таблиця відповідності двійкового чотирьохрозрядного і коду Грея (табл. 5) дозволяє встановити логічний звязок між ними.

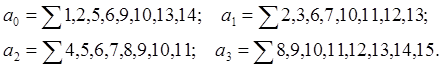
Відповідна карта Карно приведена на рис. 24.

Після мінімізації маємо:

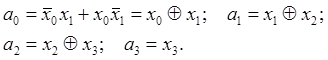
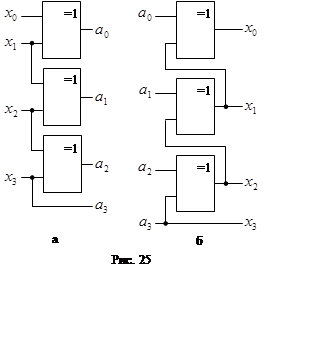
Таким чином перетворення двійкового коду в код Грея відбувається елементом ВИКЛЮЧАЮЧЕ АБО (рис. 25а).


Подпись: Двійковий код Код Грея x3 x2 x1 x0 a3 a2 a1 a0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 2 0 0 1 0 0 0 1 1 3 0 0 1 1 0 0 1 0 4 0 1 0 0 0 1 1 0 5 0 1 0 1 0 1 1 1 6 0 1 1 0 0 1 0 1 7 0 1 1 1 0 1 0 0 8 1 0 0 0 1 1 0 0 9 1 0 0 1 1 1 0 1 10 1 0 1 0 1 1 1 1 11 1 0 1 1 1 1 1 0 12 1 1 0 0 1 0 1 0 13 1 1 0 1 1 0 1 1 14 1 1 1 0 1 0 0 1 15 1 1 1 1 1 0 0 0 Табл. 5 Задача перетворення коду Грея в двійковий вирішується аналогічно. Результуюча схема перетворювача відповідає рисунку 25б.

  62. 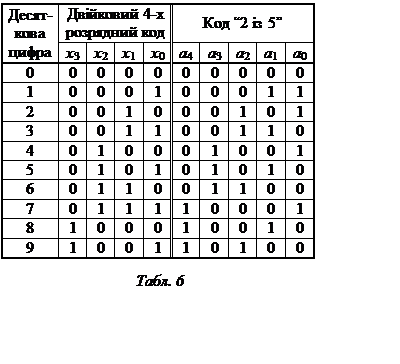 Подпись: Десят-кова цифра Двійковий 4-х розрядний код Код “2 із 5” х3 х2 х1 х0 а4 а3 а2 а1 а0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 1 2 0 0 1 0 0 0 1 0 1 3 0 0 1 1 0 0 1 1 0 4 0 1 0 0 0 1 0 0 1 5 0 1 0 1 0 1 0 1 0 6 0 1 1 0 0 1 1 0 0 7 0 1 1 1 1 0 0 0 1 8 1 0 0 0 1 0 0 1 0 9 1 0 0 1 1 0 1 0 0 Табл. 6 Код “2 з 5” використовується для безпомилкової передачі цифрової інформації. В цьому п’ятирозрядному коді кожна допустима комбінація містить дві одиниці, й оскільки таких комбінацій десять, то кожна з них відповідає одній десятковій цифрі. Так як точно дві одиниці повинні бути в цьому коді, код “2 з 5” має захист від помилок, які виникають при передачі його в цифровому каналі зв’язку. (див. табл. 6)

Мінімізуючи функції а0…а4 отримаємо вирази для вихідних сигналів:

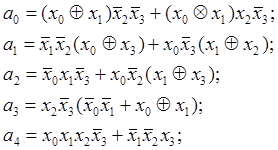
які легко реалізувати використовуючи елементи ВИКЛЮЧАЮЧЕ АБО.

  63. 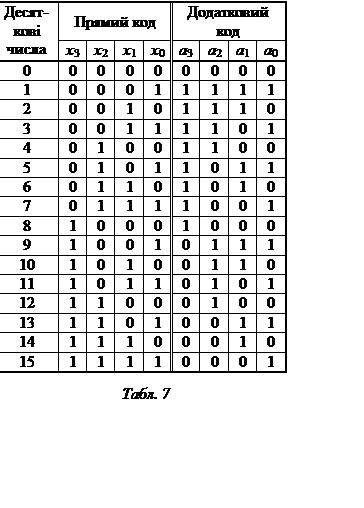 Подпись: Десят-кові числа Прямий код Додатковий код х3 х2 х1 х0 а3 а2 а1 а0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 1 1 2 0 0 1 0 1 1 1 0 3 0 0 1 1 1 1 0 1 4 0 1 0 0 1 1 0 0 5 0 1 0 1 1 0 1 1 6 0 1 1 0 1 0 1 0 7 0 1 1 1 1 0 0 1 8 1 0 0 0 1 0 0 0 9 1 0 0 1 0 1 1 1 10 1 0 1 0 0 1 1 0 11 1 0 1 1 0 1 0 1 12 1 1 0 0 0 1 0 0 13 1 1 0 1 0 0 1 1 14 1 1 1 0 0 0 1 0 15 1 1 1 1 0 0 0 1 Табл. 7 Додаткові коди утворюються із прямого Х шляхом інвертування прямого коду й додавання до нього 1 молодшого розряду . В результаті маємо таблицю відповідності кодів (табл. 7).

Мінімізуючи логічні функції а0-а3 за допомогою карт Карно находимо мінімізовані вирази вихідних функції.

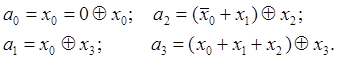
  64.  Для реалізації функції приведемо іі до досконалої дизюнктивної нормальної форми:

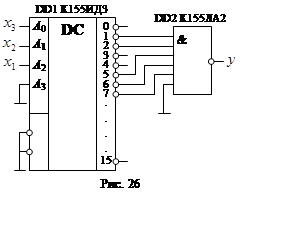
Використовуючи шестивходовий елемент К155ЛА2 І-НЕ отримуємо схему, яка буде реалізовувати захисну функцію (рис. 26).

  65. 


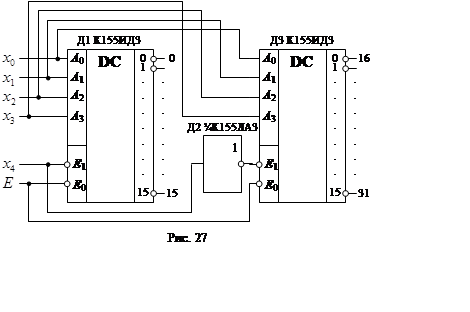
Принципова схема розроблюємого дешифратора приведена на рис/ 27 (ДД1, ДД2 – К155ИД3; ДД3 – ¼К155ЛА3).

  66. 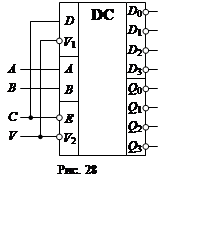 Якщо входи A, B, C використовувати як адресні (рис. 28), а інформацію подавати на вход V, данна мікросхема буде працювати як дешифратор який складається із трьох входів А, В, С на вісім виходів.

  67.  Дешифратор 564ИД1 виконує перетворення 4-х розрядного двійкового коду в вихідний сигнал високого рівня на одному з 10 виходів. Із таблиці істиності мікросхеми маємо, що при зміні двійкового коду в інтервалі значень, відповідаючих десятковим числам 0-9 має місце однозначна відповідність вхідного двійкового коду й сигналу високого рівня на відповідному виході 0-9. При значеннях вхідного двійкового коду більших 1001 виходи 0-7 мають нульовий вихідний сигнал. Таким чином мікросхема дозволяє однозначно виконувати дешифрацію трьохрозрядного двійкового коду на один з 8 виходів при наявності нуля на вході А3 (рис. 29). При наявності сигналу високого рівня на вході А3 виходи 0-7 будуть відключені. Тобто вхід А3 може виконувати функцію входу, який дозволяє роботу мікросхеми з декодування інформації, яка надходить на входи А0, А1, А2.

Скачать файл