89. Розглянути мікросхему К155ИМ3. Пояснити, як використовувати вказаний чотирьохрозрядний суматор для сумування: а) двох чотирьохрозрядних чисел; б) для сумування двох дворозрядних та двох однорозрядних; в)для сумування двох восьмирозрядних (байтових) чисел.
90. Використовуючи мікросхему К155ИМ3, розробити схему, що дозволяє здійснювати як сумування, та і віднімання напівбайтових слів.
91. Спроектувати комбінаційну схему, за допомогою якої можна здійснювати доповнення до 9 для кожної десяткової цифри.
92. Розробити перетворювач чотирьохрозрядного двійкового коду 8, 4, 2, 1 у код “з надлишком 3”.
93. Розробити пристрій двійкового множення на суматорах та логічних елементах І, що дозволяє множити чотирьохрозрядне число А на трьохрозрядне В.
94. Спроектувати схему, що дозволяє отримати квадрати будь-якого трьохрозрядного двійкового числа.
95. Використовуючи мультиплексор К155КП2, розробити принципові схеми дворозрядного суматора та дворозрядного віднімателя.
96. Використовуючи логічні елементи ВИКЛЮЧАЮЧЕ АБО та елементи заперечення, розробити дворозрядний компаратор.
97. Розробити принципову схему суматора, що дозволяє здійснювати додавання однорозрядних десяткових чисел.
98. Використовуючи результат попередньої задачі, розробити схему для додавання двох дворозрядних чисел.
99. Використовуючи чотирьохрозрядний суматор та додаткові логічні елементи, розробити схему чотирьохрозрядного компаратора.
100. З використанням чотирьохрозрядного суматора К155ИМ3, розробити схему для додавання та віднімання двох дванадцятирозрядних чисел.
101. Використовуючи чотирьохрозрядні компаратори К155ИП2, розробити схему порівняння двох дванадцятирозрядних кодів.
102. Розробити комбінаційні логічні схеми, які можуть бути використані для порівняння двох двійкових чисел А та В. Ці схеми аовинні показувати, чи є: 1. А > B; 2. A = B; 3. A < B. Розширити схеми таким чином, щоб можно було порівнювати чотирьохрозрядні числа.
103. Розробити комбінаційну логічну схему, яка дозволить здійснювати перетворення чотирьохрозрядних двійкових чисел у додатковий код.
1. 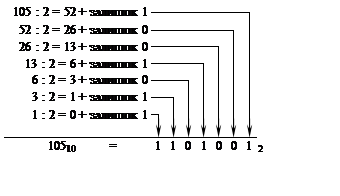 Перетворення здійснюється шляхом послідовного ділення
числа, яке представлене у десятковій системі счислення, на основу системи
счислення, в яку перетворюється число. Для перетворення у двійкову систему
счислення число 105 необхідно поетапно ділити на 2. Залишок від ділення на
кожному етапі складе двійкове число, починаючи з молодшого розряду.
Перетворення здійснюється шляхом послідовного ділення
числа, яке представлене у десятковій системі счислення, на основу системи
счислення, в яку перетворюється число. Для перетворення у двійкову систему
счислення число 105 необхідно поетапно ділити на 2. Залишок від ділення на
кожному етапі складе двійкове число, починаючи з молодшого розряду.
2. 11810 = 011101102; 5710 = 001110012; 19610 = 110001002; 23810 = 111011102 .
3.
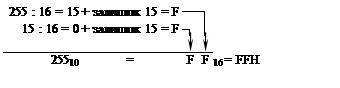 |
395910 = 9A5F16
4.
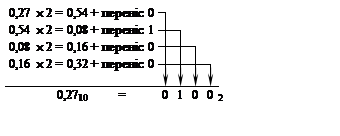 |
0,62510 = 0,1012
5.
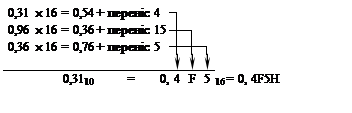 |
6. Вказівка. Перетворення десяткових чисел, які містять цілу та дрібну частину, здійснюється окремо для кожної з них.
Відповідь: 25,17910 = 11001,0010012.
7. 69.4210 = 45.6В8516
8.
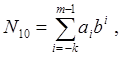 |
|||
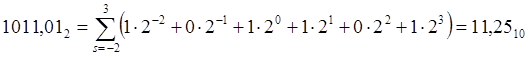 |
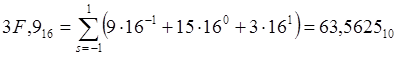 |
9.
10.
Якщо в результаті роздроблення двійкового числа на тетрадр утворюються неповні тетради, їх небхідно доповнити нулями: цілу частину в сторону старших розрядів; дробну — в сторону молодших.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.