28.
 |
|
Рис. 5 |

 |
||||
|
||||
|
||||


29.
30.
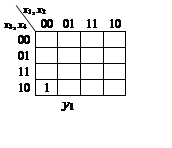 |
 |
 |
31. ![]()
![]()
![]()
![]()
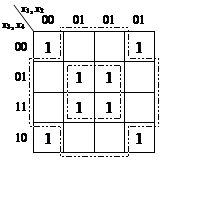 Мінімізація здійснюється
шляхом об’єднання сусідніх клітинок карти, відповідних
одиничним (нулевим) значенням функції, і записи функції, як незмінних
координат об’єднаних клітинок. Для функції, представленої на рис. 1а маємо
об’єднання, відповідне до рис. 8а. З рис. 8а. Виходить . Мінімізовані функції:
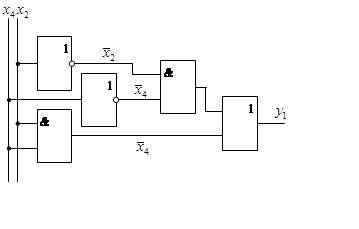
. На рис. 8б наведен приклад реалізації
у1.
Мінімізація здійснюється
шляхом об’єднання сусідніх клітинок карти, відповідних
одиничним (нулевим) значенням функції, і записи функції, як незмінних
координат об’єднаних клітинок. Для функції, представленої на рис. 1а маємо
об’єднання, відповідне до рис. 8а. З рис. 8а. Виходить . Мінімізовані функції:
. На рис. 8б наведен приклад реалізації
у1.
32. ![]()
![]()
![]()
![]()
![]()
![]()
33. Функції істиності наведені в таблиці 2.
Таблиця 2
|
Входи |
М2 x1Åx2Åx3 |
Нерівність (неспівпадіня) |
Виключаюче АБО (один і тільки один) |
Диз’юнкція (АБО) |
||
|
x3 |
x2 |
x1 |
||||
|
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
0 1 1 0 1 0 0 1 |
0 1 1 1 1 1 1 0 |
0 1 1 0 1 0 0 0 |
0 1 1 1 1 1 1 1 |
Таблиці істинності всіх чотирьох функцій різні, що каже про те, що при трьох і більш аргументах це зовсім різні функції. В той же час будучи побудованними для двох аргументів, таблиці перших трьох функцій повністю співпадають, чим і поясняються три майже однакові розповсюджені назви функцій М2: сума за модулем 2; нерівнозначність, виключаюче АБО.
34. ![]()
35. 1. ![]()
![]()
![]()
![]()
2. ![]()
3. ![]()
![]()
4. ![]()
36. ![]()
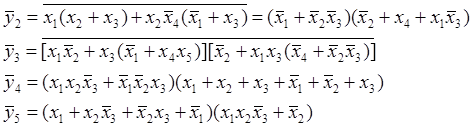
37. Вказівка. Перед складанням таблиць функції приводяться до досконалих диз’юнктивних нормальних форм.
38. ![]()
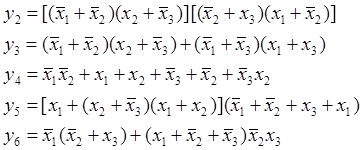
39. Приводимо функцію до досконалої диз’юнктивної нормальної форми:
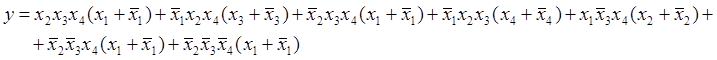
 Після перетворень та виключень повторюючихся
членів (мінтермів) знаходимо:
Після перетворень та виключень повторюючихся
членів (мінтермів) знаходимо:
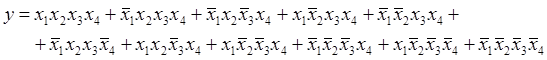
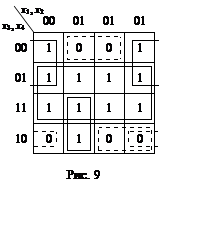
Підставляючи значення функції у
відповідні клітинки карти Карно та об’єднуючи сусідні клітинки групами по 2, 4,
8 (рис. 9), знаходимо ![]() .
.
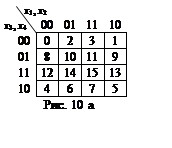 Карта Карно дозволяє також провести мінімізацію
тієї ж функції у кон’юктивній нормальній формі, об’єднуючи нульові значення
мінтермів (об’єднання виконані шриховими лініями).
Карта Карно дозволяє також провести мінімізацію
тієї ж функції у кон’юктивній нормальній формі, об’єднуючи нульові значення
мінтермів (об’єднання виконані шриховими лініями).
![]()
![]()
40.  Будь-який мінтерм чотирьох логічних змінних
записати, починаючи зі старших логічних змінних. Наприклад –
Будь-який мінтерм чотирьох логічних змінних
записати, починаючи зі старших логічних змінних. Наприклад – ![]() . Враховуючи, що
. Враховуючи, що ![]() ,
, ![]() , можна стверджувати:
, можна стверджувати: ![]() .
.
Звідси кожній клітинці карти Карно відповідатиме свій номер десяткової чи шістнадцяткової системи счислення. На рис. 10а приведена нумерація клітинок, яка відповідає розташуванню на ній та значенням логічних елементів.
 Звідси випливає, що логічна функція може бути
задана перерахуванням клітинок, які відповідають істинним значенням мінтермів.
Звідси випливає, що логічна функція може бути
задана перерахуванням клітинок, які відповідають істинним значенням мінтермів.
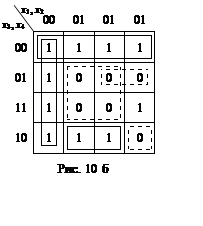
Для функції у1 = f(x1, x2, x3, x4) карта Карно відповідатиме рис. 10б.
Як відмічалося у №39, мінімізована функція може бути отримана як шляхом об’єднання клітинок з записаними у ній одиницями, так і з нулями.
В результаті мінімізації знаходимо:
![]()
41. ![]()
![]() .
.
Аналогічно розв’язуються й інші приклади.
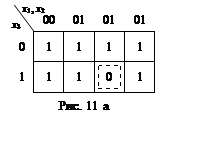
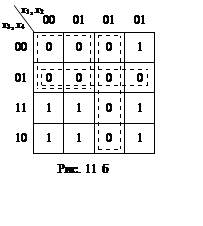
43. Для функції у1 карта
Карно відповідає рис. 11а; для функції у2 – рис. 11б. Після
мінімізації маємо: ![]()
 Функція у1 просто реалізується на трьохвхідному
елементі І-НЕ: – 3І-НЕ.
Функція у1 просто реалізується на трьохвхідному
елементі І-НЕ: – 3І-НЕ.
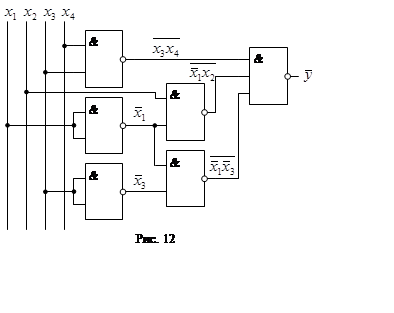
Функція у2 перетворюємо у наступній послідовності:
![]()
Отриманий результат дозволяє реалізувати її у базисі І-НЕ (рис. 12).
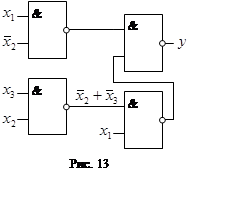
44. Функцію у1 представимо
у вигляді: ![]()
Остання форма представлення дозволяє розв’язати задачу реалізації логічної функції (рис. 13).
 Аналогічно виконаємо перетворення функції
у2:
Аналогічно виконаємо перетворення функції
у2:
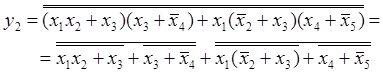
Введемо позначення:
![]()
Тоді ![]()
Деталізуємо складові а1, b1:
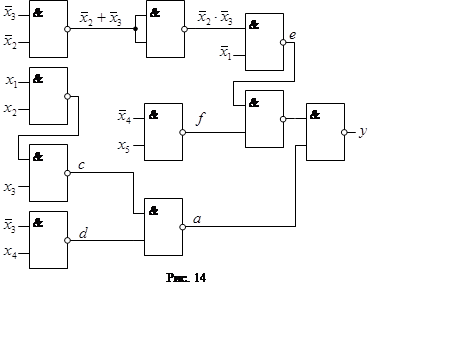
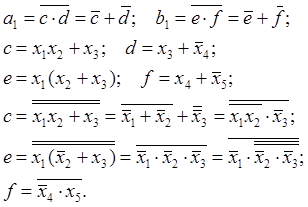
На рис. 14 приведена принципова схема логічного пристрою, що реалізує функцію у2 у базисі І-НЕ.
45. ![]()
![]()
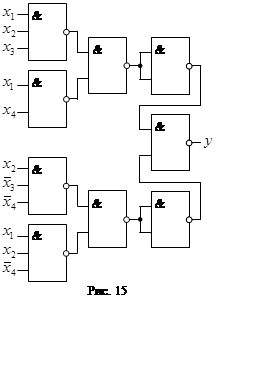 Приклад реалізації
приведен на рис. 15.
Приклад реалізації
приведен на рис. 15.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.