 5. Груз А массы
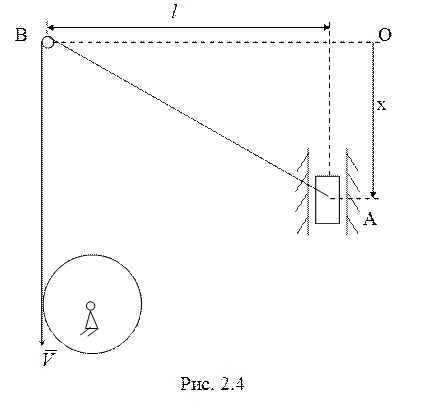
5. Груз А массы ![]() поднимается по вертикальному стержню с
помощью нерастяжимого троса, перекинутого через блок В пренебрежимо малых размеров,
отстоящий от стержня на расстояние
поднимается по вертикальному стержню с
помощью нерастяжимого троса, перекинутого через блок В пренебрежимо малых размеров,
отстоящий от стержня на расстояние ![]() (рис. 2.4). Трос
наматывается на барабан с постоянной скоростью
(рис. 2.4). Трос
наматывается на барабан с постоянной скоростью ![]() .
. ![]() - коэффициент трения скольжения груза по
стержню. Найти натяжение троса в точке А в зависимости от координаты поднимаемого
груза
- коэффициент трения скольжения груза по
стержню. Найти натяжение троса в точке А в зависимости от координаты поднимаемого
груза ![]() . (5 баллов)
. (5 баллов)
 6. Материальная
точка одета на неподвижное кольцо радиуса
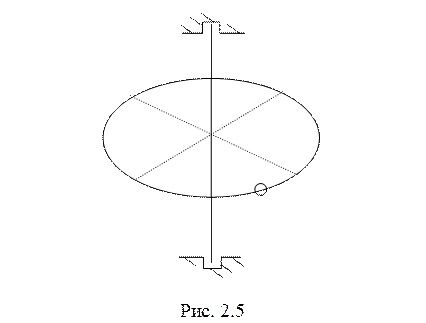
6. Материальная
точка одета на неподвижное кольцо радиуса ![]() , закрепленное
в горизонтальной плоскости (рис. 2.5). Коэффициент трения между точкой и
кольцом равен
, закрепленное
в горизонтальной плоскости (рис. 2.5). Коэффициент трения между точкой и
кольцом равен ![]() . Какую начальную скорость
. Какую начальную скорость ![]() нужно сообщить точке, чтобы она могла совершить
по кольцу полный оборот? (7 баллов)
нужно сообщить точке, чтобы она могла совершить
по кольцу полный оборот? (7 баллов)
 7. Тонкий однородный
стержень длины
7. Тонкий однородный
стержень длины ![]() помещен вертикально в воду в состояние
покоя (рис. 2.6) так, что верхний конец стержня удален от поверхности воды на расстояние
помещен вертикально в воду в состояние
покоя (рис. 2.6) так, что верхний конец стержня удален от поверхности воды на расстояние
![]() . Плотность материала стержня в два раза
меньше плотности воды. Пренебрегая сопротивлением воды, найти наибольшую высоту
подъема верхнего конца стержня над поверхностью воды. (7 баллов)
. Плотность материала стержня в два раза
меньше плотности воды. Пренебрегая сопротивлением воды, найти наибольшую высоту
подъема верхнего конца стержня над поверхностью воды. (7 баллов)
8. Однородный
горизонтальный диск массы ![]() и радиуса
и радиуса ![]() может без трения вращаться вокруг
вертикальной неподвижной оси
может без трения вращаться вокруг
вертикальной неподвижной оси ![]() (рис. 2.7). По диску
движется материальная точка М массы
(рис. 2.7). По диску
движется материальная точка М массы ![]() согласно уравнениям
согласно уравнениям 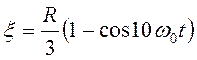 ,
, 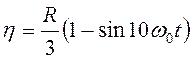 в
прямоугольных осях координат, жестко связанных с диском. В начальный момент времени
угловая скорость диска
в
прямоугольных осях координат, жестко связанных с диском. В начальный момент времени
угловая скорость диска ![]() . Найти угловую скорость диска в
те моменты времени, когда точка М наиболее близка к центру диска и наиболее
удалена от него. (10 баллов)
. Найти угловую скорость диска в
те моменты времени, когда точка М наиболее близка к центру диска и наиболее
удалена от него. (10 баллов)
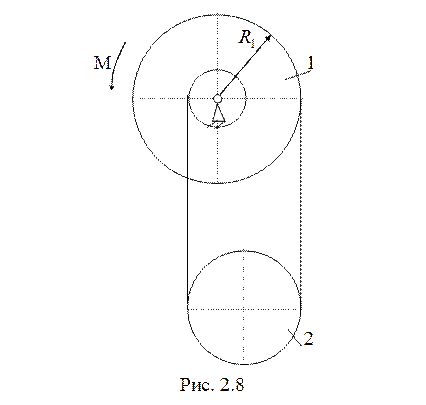 9. Однородный диск 1
массы
9. Однородный диск 1
массы ![]() и радиуса
и радиуса ![]() имеет
цилиндрический выступ пренебрежимо малой массы (рис. 2.8). Невесомая и
нерастяжимая нить охватывает ступени диска 1 и однородный диск 2 массы
имеет
цилиндрический выступ пренебрежимо малой массы (рис. 2.8). Невесомая и
нерастяжимая нить охватывает ступени диска 1 и однородный диск 2 массы ![]() и радиуса
и радиуса ![]() . Найти
угловое ускорение диска 1 при действии на него вращающего момента
. Найти
угловое ускорение диска 1 при действии на него вращающего момента ![]() . Трением в оси вращения пренебречь. Проскальзывание
нити по дискам и отклонение свободных участков нити от вертикали отсутствует.
(6 баллов)
. Трением в оси вращения пренебречь. Проскальзывание
нити по дискам и отклонение свободных участков нити от вертикали отсутствует.
(6 баллов)
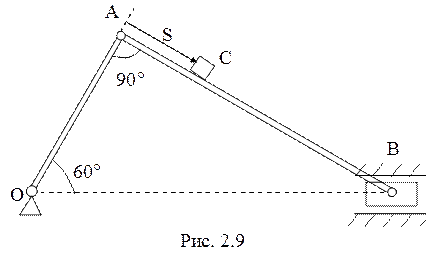
10. Из точки А с нулевой
начальной скоростью по стержню АВ за счет сил взаимодействия со стержнем
движется точка С (рис. 2.9) массы ![]() . Стержни расположены в
вертикальной плоскости. Массы однородных стержней ОА и АВ равны
. Стержни расположены в
вертикальной плоскости. Массы однородных стержней ОА и АВ равны ![]() и
и ![]() соответственно,
масса ползуна В равна
соответственно,
масса ползуна В равна ![]() . Длина
. Длина ![]() .
Найти закон движения точки С, при котором стержни в указанном положении остаются
неподвижными. Трением в шарнирах и направляющих ползуна пренебречь. (7 баллов)
.
Найти закон движения точки С, при котором стержни в указанном положении остаются
неподвижными. Трением в шарнирах и направляющих ползуна пренебречь. (7 баллов)
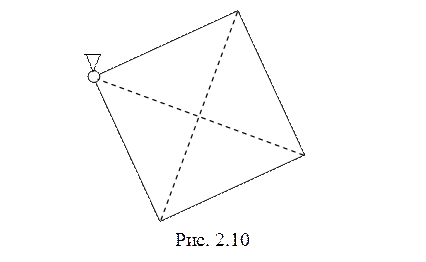 11. Однородная
квадратная пластина со стороной
11. Однородная
квадратная пластина со стороной ![]() (рис. 2.10) качается
относительно горизонтальной оси, перпендикулярной плоскости пластины и
проходящей через ее вершину, без трения. В какой точке пластины следует
поместить точечную массу, чтобы закон движения пластины не изменился при
сохранении тех же начальных условий? (6 баллов)
(рис. 2.10) качается
относительно горизонтальной оси, перпендикулярной плоскости пластины и
проходящей через ее вершину, без трения. В какой точке пластины следует
поместить точечную массу, чтобы закон движения пластины не изменился при
сохранении тех же начальных условий? (6 баллов)
12. Однородный сплошной
диск массы ![]() и радиуса
и радиуса ![]() лежит
своей плоскостью на гладкой горизонтальной плоскости. По ободу диска движется
материальная точка той же массы
лежит
своей плоскостью на гладкой горизонтальной плоскости. По ободу диска движется
материальная точка той же массы ![]() со скоростью
со скоростью ![]() относительно диска. В начальный момент
времени система покоилась. Найти скорость центра диска. (7 баллов)
относительно диска. В начальный момент
времени система покоилась. Найти скорость центра диска. (7 баллов)
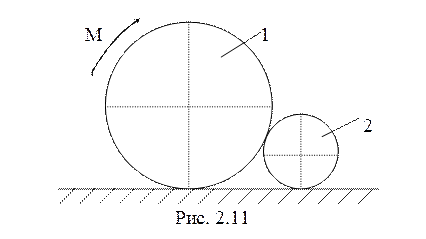 13. Два однородных
соприкасающихся цилиндрических катка катятся без проскальзывания по достаточно
шероховатой горизонтальной плоскости под действием момента
13. Два однородных
соприкасающихся цилиндрических катка катятся без проскальзывания по достаточно
шероховатой горизонтальной плоскости под действием момента ![]() , приложенного к первому катку
, приложенного к первому катку
(рис. 2.11). Найти силы взаимодействия
между катками, если для их масс ![]() , радиусы
, радиусы ![]() , а коэффициент трения скольжения между
катками
, а коэффициент трения скольжения между
катками ![]() . При каком значении момента
. При каком значении момента ![]() первый каток не отрывается от
горизонтальной плоскости. Трением качения пренебречь. (8 баллов)
первый каток не отрывается от
горизонтальной плоскости. Трением качения пренебречь. (8 баллов)
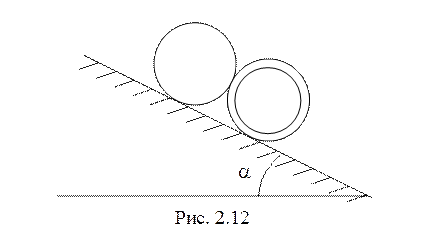 14. По шероховатой
наклонной плоскости, образующей угол
14. По шероховатой
наклонной плоскости, образующей угол ![]() с горизонтом, без проскальзывания катятся,
примыкая друг к другу, однородные сплошной и полый цилиндры одинаковой массы
с горизонтом, без проскальзывания катятся,
примыкая друг к другу, однородные сплошной и полый цилиндры одинаковой массы ![]() и радиуса
и радиуса ![]() (рис.
2.12). Коэффициент трения между цилиндрами и между каждым из них и плоскостью
(рис.
2.12). Коэффициент трения между цилиндрами и между каждым из них и плоскостью ![]() . Найти ускорение центров цилиндров, их
силы давления друг на друга и значение угла
. Найти ускорение центров цилиндров, их
силы давления друг на друга и значение угла ![]() , при
котором возможно качение по плоскости без проскальзывания. (12 баллов)
, при
котором возможно качение по плоскости без проскальзывания. (12 баллов)
 15. Каким условиям
должен удовлетворять постоянный вращающий момент
15. Каким условиям
должен удовлетворять постоянный вращающий момент ![]() , чтобы
с его помощью можно было однородный сплошной цилиндр радиуса
, чтобы
с его помощью можно было однородный сплошной цилиндр радиуса ![]() и массы
и массы ![]() вкатить
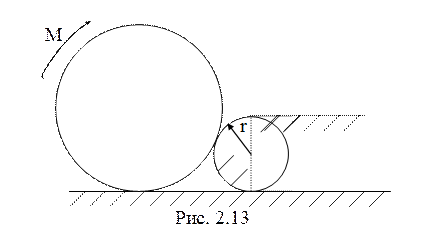
из состояния покоя на выступ круговой формы радиуса
вкатить
из состояния покоя на выступ круговой формы радиуса ![]() без
проскальзывания (рис. 2.13)?
без
проскальзывания (рис. 2.13)? ![]() , коэффициент трения
скольжения равен
, коэффициент трения
скольжения равен ![]() . Трением качения пренебречь. (17
баллов)
. Трением качения пренебречь. (17
баллов)
16. Материальная точка А
массы ![]() скользит по гладким горизонтальным
направляющим и соединена с грузом В массы
скользит по гладким горизонтальным
направляющим и соединена с грузом В массы ![]() невесомой
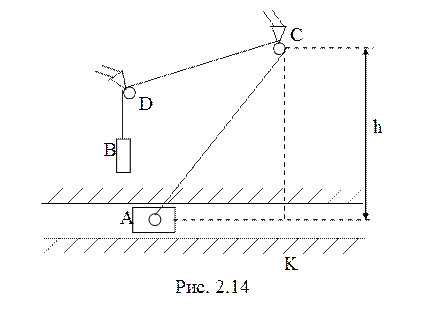
нерастяжимой нитью, перекинутой через точечные блоки С и D (рис. 2.14).
невесомой
нерастяжимой нитью, перекинутой через точечные блоки С и D (рис. 2.14). ![]() -
высота блока С над направляющими. В начальный момент времени расстояние
-
высота блока С над направляющими. В начальный момент времени расстояние ![]() и система покоилась. Найти, с какой скоростью
точка А попадет в точку К. Трением в осях блоков пренебречь. (5 баллов)
и система покоилась. Найти, с какой скоростью
точка А попадет в точку К. Трением в осях блоков пренебречь. (5 баллов)
 17. Точечный груз
массы
17. Точечный груз
массы ![]() съезжает по гладкой цилиндрической поверхности
радиуса
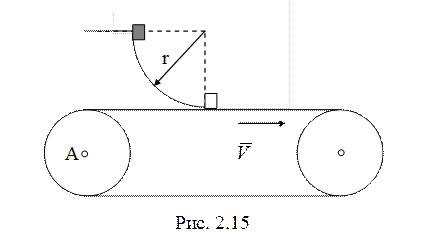
съезжает по гладкой цилиндрической поверхности
радиуса ![]() (рис. 2.15), начиная движение из состояния
покоя в верхней точке. В низшей точке груз попадает на шероховатую ленту
транспортера, движущуюся со скоростью
(рис. 2.15), начиная движение из состояния
покоя в верхней точке. В низшей точке груз попадает на шероховатую ленту
транспортера, движущуюся со скоростью ![]() . Коэффициент
трения между лентой и грузом равен
. Коэффициент
трения между лентой и грузом равен ![]() . Найти путь скольжения
груза относительно ленты. (5 баллов).
. Найти путь скольжения
груза относительно ленты. (5 баллов).
18. Шарнирно соединенные
одинаковые однородные стержни длины ![]() симметрично опираются
на две гладкие тумбы, расстояние между которыми
симметрично опираются
на две гладкие тумбы, расстояние между которыми ![]()
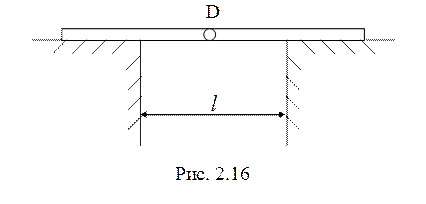 (рис. 2.16). В начальный момент
времени стержни были горизонтальны и покоились, а затем начали падать. Трение в
шарнире отсутствует. Считая, что масса стержней такова, что они не отрываются
от тумб, найти скорость точки D в
тот момент времени, когда концы стержней достигнут угловых точек тумб. (7 баллов)
(рис. 2.16). В начальный момент
времени стержни были горизонтальны и покоились, а затем начали падать. Трение в
шарнире отсутствует. Считая, что масса стержней такова, что они не отрываются
от тумб, найти скорость точки D в
тот момент времени, когда концы стержней достигнут угловых точек тумб. (7 баллов)
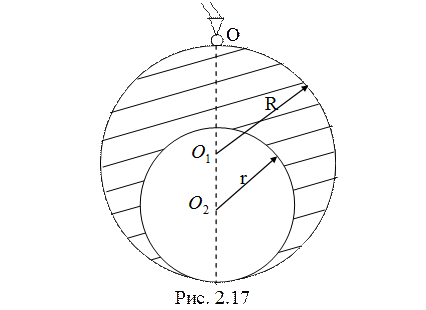
19. Пластина представляет
собой однородный диск радиуса ![]() с круговым отверстием
радиуса
с круговым отверстием
радиуса ![]() (рис. 2.17), расположенный в вертикальной
плоскости.
(рис. 2.17), расположенный в вертикальной
плоскости.
1) Какую начальную
угловую скорость ![]() нужно сообщить пластине, чтобы
ее максимальный угол отклонения из положения устойчивого равновесия составил
нужно сообщить пластине, чтобы
ее максимальный угол отклонения из положения устойчивого равновесия составил ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.