1. Краткие сведения из теории
1.1. Динамика материальной точки
Основным уравнением в динамике материальной точки относительно инерциальной системы отсчета (принятой за покоящуюся или прямолинейно равномерно движущуюся) является второй закон Ньютона
![]() (1.1)
(1.1)
(![]() – масса
точки,
– масса
точки, ![]() - ее ускорение,
- ее ускорение, ![]() -
сумма действующих на точку сил). Через радиус-вектор, характеризующий положение
точки, он записывается в виде
-
сумма действующих на точку сил). Через радиус-вектор, характеризующий положение
точки, он записывается в виде
![]() . (1.2)
. (1.2)
Если при известной массе
![]() и законе движения точки
и законе движения точки ![]() нужно найти силы, под действием которых
точка совершает заданное движение, то это первая, или прямая задача динамики.
Она решается непосредственным применением формулы
нужно найти силы, под действием которых
точка совершает заданное движение, то это первая, или прямая задача динамики.
Она решается непосредственным применением формулы
![]() .
.
Если при известной массе
точки и действующих на точку силах нужно найти закон движения точки ![]() (вторая, или обратная, задача динамики),
то необходимо решить дифференциальное уравнение (1.2) относительно радиус вектора
(вторая, или обратная, задача динамики),
то необходимо решить дифференциальное уравнение (1.2) относительно радиус вектора
![]() . Общее решение этого уравнения второго
порядка определяется с точностью до двух векторных произвольных постоянных, для
нахождения которых требуется задать некоторые два условия. Таковыми, если их
можно сформулировать, чаще всего являются начальные условия, задающие
. Общее решение этого уравнения второго
порядка определяется с точностью до двух векторных произвольных постоянных, для
нахождения которых требуется задать некоторые два условия. Таковыми, если их
можно сформулировать, чаще всего являются начальные условия, задающие ![]() и
и ![]() в
начальный момент времени (т.е. начальное положение точки и ее начальную
скорость). Тогда постановка задачи принимает вид
в
начальный момент времени (т.е. начальное положение точки и ее начальную
скорость). Тогда постановка задачи принимает вид
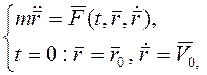 (1.3)
(1.3)
что представляет собой задачу Коши, имеющую единственное решение при достаточно гладкой правой части дифференциального уравнения.
В проекциях на оси
декартовой системы координат ![]() (1.3) принимает вид
(1.3) принимает вид
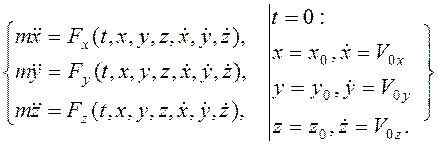 (1.4)
(1.4)
При свободном плоском движении точки
достаточно использовать две оси ![]() и
и ![]() , при прямолинейном движении – только ось
, при прямолинейном движении – только ось ![]() . Система (1.3) может также быть записана в
проекциях на оси некоторой другой системы координат. Способ решения
составленной системы дифференциальных уравнений зависит от вида ее правой
части, т.е. от характера действующих сил.
. Система (1.3) может также быть записана в
проекциях на оси некоторой другой системы координат. Способ решения
составленной системы дифференциальных уравнений зависит от вида ее правой
части, т.е. от характера действующих сил.
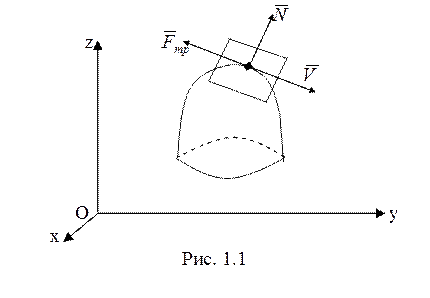 При движении точки по
неподвижной поверхности, описываемой уравнением
При движении точки по
неподвижной поверхности, описываемой уравнением ![]() (рис.
1.1), действующие на точку силы представи-мы в виде
(рис.
1.1), действующие на точку силы представи-мы в виде ![]() , где
, где ![]() – сумма приложенных к точке активных сил,
нормальная реакция поверхности
– сумма приложенных к точке активных сил,
нормальная реакция поверхности ![]() ; сила трения, направленная
против скорости движения точки
; сила трения, направленная
против скорости движения точки ![]() (
(![]() – коэффициент трения скольжения). Уравнения
из системы (1.4) тогда принимают вид
– коэффициент трения скольжения). Уравнения
из системы (1.4) тогда принимают вид
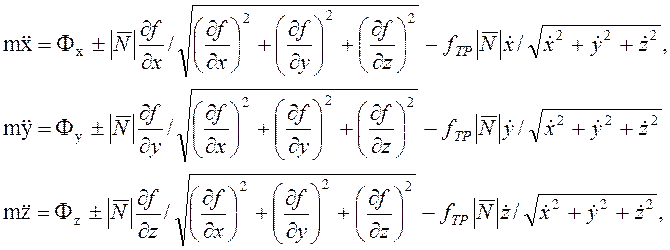
они решаются совместно с уравнением
поверхности ![]() .
.
В траекторных
координатах (рис. 1.2) ускорение 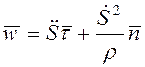
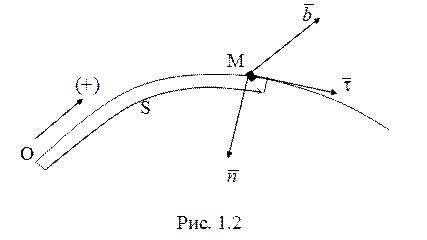 (
(![]() -
радиус кривизны траектории), и (1.1) в проекциях на касательную, нормаль и бинормаль
принимает вид
-
радиус кривизны траектории), и (1.1) в проекциях на касательную, нормаль и бинормаль
принимает вид
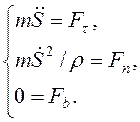
Для неинерциальной системы отсчета обобщением (1.1) является динамическая теорема Кориолиса
![]() , (1.5)
, (1.5)
где ![]() -
ускорение точки относительно неинерциальной системы отсчета,
-
ускорение точки относительно неинерциальной системы отсчета, ![]() - переносная сила инерции,
- переносная сила инерции, ![]() - кориолисова сила инерции. Проецирование
(1.5) на оси координат дает дифференциальные уравнения, описывающие движение
точки (аналогично инерциальной системе отсчета).
- кориолисова сила инерции. Проецирование
(1.5) на оси координат дает дифференциальные уравнения, описывающие движение
точки (аналогично инерциальной системе отсчета).
1.2. Основные теоремы динамики
При составлении уравнений, описывающих динамику точки и системы, могут использоваться основные теоремы динамики. Выбор той или иной теоремы при решении задачи обусловлен постановкой задачи, особенностями движения системы и тем, какая теорема динамики позволяет исключить из составляемых уравнений заранее неизвестные силы реакции связей.
1.Теорема о движении центра масс системы.
Радиус-вектор центра масс системы удовлетворяет соотношению
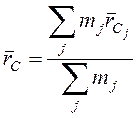 ,
,
где ![]() -
радиус-векторы центров масс отдельных тел, входящих в систему. Для твердого
тела массы
-
радиус-векторы центров масс отдельных тел, входящих в систему. Для твердого
тела массы ![]()
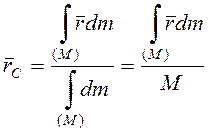 .
.
Согласно теореме о движении центра масс
![]() , (1.6)
, (1.6)
где ![]() – масса
всей системы,
– масса
всей системы, ![]() - главный вектор приложенных к
системе внешних сил.
- главный вектор приложенных к
системе внешних сил.
Если ![]() , то скорость центра масс системы
, то скорость центра масс системы ![]() .Если не только
.Если не только ![]() , но и
начальная скорость центра масс
, но и
начальная скорость центра масс ![]() , то
, то ![]() , т.е. положение центра масс системы
остается неизменным. Все вышеприведенные формулы и утверждения можно выписать в
проекциях на оси координат
, т.е. положение центра масс системы
остается неизменным. Все вышеприведенные формулы и утверждения можно выписать в
проекциях на оси координат ![]() .
.
2. Теорема об изменении количества движения, или импульса
Импульс материальной
точки ![]() . Импульс твердого тела
. Импульс твердого тела 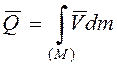 . Импульс системы выражается через движение
центра масс согласно формуле
. Импульс системы выражается через движение
центра масс согласно формуле ![]() . По теореме об
изменении импульса системы
. По теореме об
изменении импульса системы ![]() , или
, или 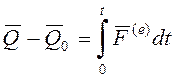 .
.
Если ![]() (система изолирована), то
(система изолирована), то ![]() . Если
. Если 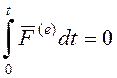 , то
, то ![]() в этот момент времени
в этот момент времени ![]() .
.
Соответствующие выражения
можно получить проецированием приведенных формул на оси координат ![]() .
.
3.Теорема об изменении кинетического момента
Кинетическим моментом
материальной точки относительно полюса О называется следующая величина: ![]() .
.
 Для твердого тела
Для твердого тела 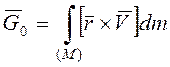 .
.
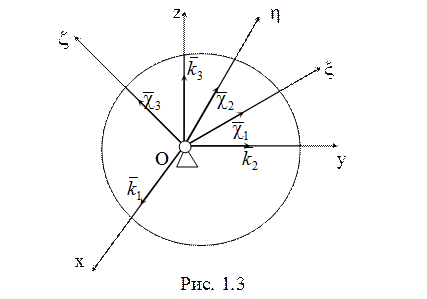
При вращении тела около неподвижной точки (рис. 1.3), если ![]() , а угловая скорость
, а угловая скорость ![]() , то
, то 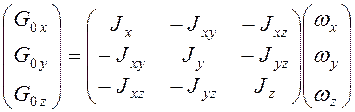 (1.7)
(1.7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.