 При
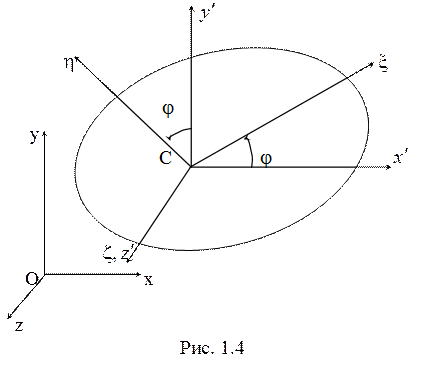
плоскопараллельном движении (рис. 1.4) теорема о движении центра масс в
проекции на оси
При
плоскопараллельном движении (рис. 1.4) теорема о движении центра масс в
проекции на оси ![]() ,
, ![]() и
теорема об изменении кинетического момента относительно центра масс в проекции
на ось
и
теорема об изменении кинетического момента относительно центра масс в проекции
на ось ![]() дают систему уравнений
дают систему уравнений
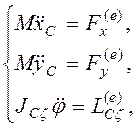
решение которой ![]() полностью описывает плоскопараллельное движение.
полностью описывает плоскопараллельное движение.
1.3. Уравнения Лагранжа второго рода
Движение механической
системы с ![]() степенями свободы однозначно описывается
зависимостью от времени некоторых независимых величин
степенями свободы однозначно описывается
зависимостью от времени некоторых независимых величин ![]() ,
называемых обобщенными координатами. Для систем с идеальными и голономными
связями дифференциальные уравнения в обобщенных координатах могут быть
составлены как уравнения Лагранжа второго рода
,
называемых обобщенными координатами. Для систем с идеальными и голономными
связями дифференциальные уравнения в обобщенных координатах могут быть
составлены как уравнения Лагранжа второго рода
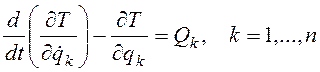 . (1.12)
. (1.12)
Голономность связи означает
независимость уравнений связи от производных по времени, а идеальность –
равенство нулю суммарной виртуальной работы (работы на виртуальных перемещениях
![]() ) сил реакции связей, приложенных к
системе:
) сил реакции связей, приложенных к
системе:
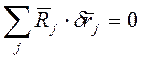 .
.
Виртуальные перемещения представляют собой воображаемые бесконечно малые перемещения, допустимые наложенными на систему связями при условии, что в уравнениях связей зафиксировано время.
Если виртуальную работу приложенных к системе сил выразить через обобщенные координаты
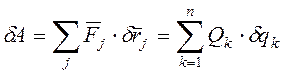 ,
,
то коэффициенты ![]() называются обобщенными силами (именно они
присутствуют в правых частях уравнений (1.12)). Обобщенная сила зависит от вида
соответствующей ей выбранной обобщенной координаты. Она представляет собой величину,
виртуальная работа которой направлена на изменение этой обобщенной координаты
при фиксированных остальных обобщенных координатах.
называются обобщенными силами (именно они
присутствуют в правых частях уравнений (1.12)). Обобщенная сила зависит от вида
соответствующей ей выбранной обобщенной координаты. Она представляет собой величину,
виртуальная работа которой направлена на изменение этой обобщенной координаты
при фиксированных остальных обобщенных координатах.
Имеет место формула 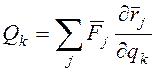 . Если виртуальную работу совершают только
консервативные силы, то
. Если виртуальную работу совершают только
консервативные силы, то 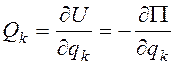 .
.
Уравнения малых колебаний системы представляют собой линеаризованные в окрестности положения устойчивого равновесия дифференциальные уравнения движения системы. Будучи линейными, они допускают аналитическое решение.
1.4. Удар
При ударе рассматривается
ничтожно малый промежуток времени, в течение которого действуют скачкообразно
меняющиеся силы, называемые ударными силами. В уравнениях, характерных для
удара, присутствуют не сами эти силы, а их ударные импульсы за время удара ![]() :
: 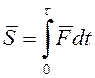 .
Членами, содержащими неударные силы (точнее их импульсы) при составлении
уравнений пренебрегают как достаточно малыми. Предполагается, что положение
системы за время удара не меняется, а скорости точек системы меняются
скачкообразно. Уравнения составляются на основе теорем динамики при ударе,
индекс "+" или "–" означает рассматриваемую величину
непосредственно после и до удара соответственно.
.
Членами, содержащими неударные силы (точнее их импульсы) при составлении
уравнений пренебрегают как достаточно малыми. Предполагается, что положение
системы за время удара не меняется, а скорости точек системы меняются
скачкообразно. Уравнения составляются на основе теорем динамики при ударе,
индекс "+" или "–" означает рассматриваемую величину
непосредственно после и до удара соответственно.
Теорема об изменении импульса имеет вид
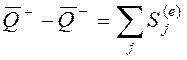 ;
;
теорема об изменении кинетического момента:
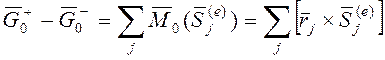
(в правой части – сумма моментов внешних ударных импульсов относительно точки О); теорема об изменении кинетической энергии
![]() ,
,
работа ударных импульсов 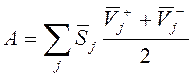 , где
, где ![]() -
скорость точки приложения ударного импульса.
-
скорость точки приложения ударного импульса.
К приведенным уравнениям может быть добавлено соотношение, отражающее гипотезу Ньютона при соударении тел (рис. 1.5)
![]() ,
,
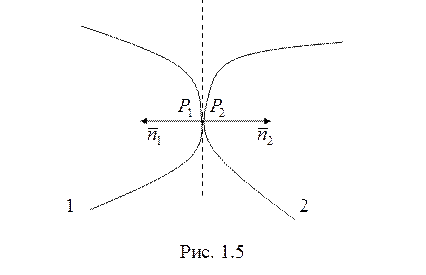 где
где ![]() (т.е. нормальная составляющая
относительной скорости точки соударения одного из тел относительно другого
тела);
(т.е. нормальная составляющая
относительной скорости точки соударения одного из тел относительно другого
тела); ![]() – единичные векторы нормали к касательной плоскости в точке
соударения тел.
– единичные векторы нормали к касательной плоскости в точке
соударения тел.
Коэффициент восстановления
![]() . При абсолютно неупругом ударе
. При абсолютно неупругом ударе ![]() , при абсолютно упругом ударе
, при абсолютно упругом ударе ![]() .
.
Уравнения Лагранжа второго рода при ударе имеют вид
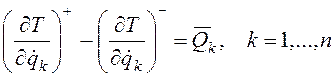 ,
,
где 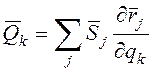 -
обобщенные ударные импульсы, соответствующие обобщенным координатам.
-
обобщенные ударные импульсы, соответствующие обобщенным координатам.
2. Условия задач
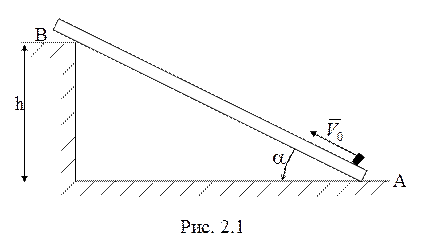 1. Однородная тонкая
доска длины
1. Однородная тонкая
доска длины ![]() (рис. 2.1) опирается на гладкий пол и на
выступ высоты
(рис. 2.1) опирается на гладкий пол и на
выступ высоты ![]() . Масса доски
. Масса доски ![]() , угол между доской и полом равен
, угол между доской и полом равен ![]() . Из точки А по доске с начальной скоростью
. Из точки А по доске с начальной скоростью
![]() начинает бежать мышь массы
начинает бежать мышь массы ![]() , принятая за материальную точку.
, принятая за материальную точку.
1) Найти закон движения мыши по доске при котором доска остается неподвижной.
2) При какой начальной
скорости ![]() мышь попадает при этом в точку В с нулевой
скоростью? (10 баллов)
мышь попадает при этом в точку В с нулевой
скоростью? (10 баллов)
2.Материальная точка
массы ![]() , имеющая начальную скорость
, имеющая начальную скорость ![]() , движется по негладкому неподвижному шару
с коэффициентом трения
, движется по негладкому неподвижному шару
с коэффициентом трения ![]() , притягиваясь к его центру силой
, притягиваясь к его центру силой
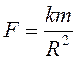 (
(![]() –
радиус шара,
–
радиус шара, ![]() ). Найти время, прошедшее от
начала движения до остановки точки. (7 баллов)
). Найти время, прошедшее от
начала движения до остановки точки. (7 баллов)
 3. Материальная точка
массы
3. Материальная точка
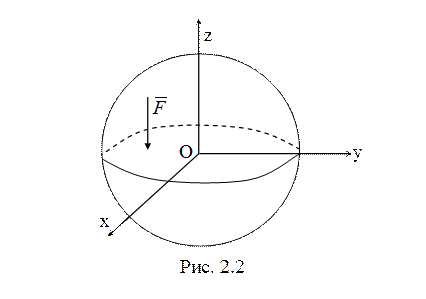
массы ![]() движется без отрыва по поверхности гладкой сферы
движется без отрыва по поверхности гладкой сферы ![]() и притягивается к плоскости
и притягивается к плоскости ![]() силой
силой 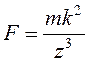 , направленной перпендикулярно этой
плоскости (рис. 2.2). В начальный момент времени точка находилась в положении
, направленной перпендикулярно этой
плоскости (рис. 2.2). В начальный момент времени точка находилась в положении ![]() и имела скорость
и имела скорость ![]() , сонаправленную с осью
, сонаправленную с осью ![]() ;
; 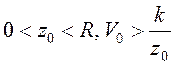 . Найти силу реакции сферы и проекцию
траектории точки на плоскость
. Найти силу реакции сферы и проекцию
траектории точки на плоскость ![]() . Силу тяжести не учитывать. (8 баллов)
. Силу тяжести не учитывать. (8 баллов)
 4. Тяжелая материальная
точка массы
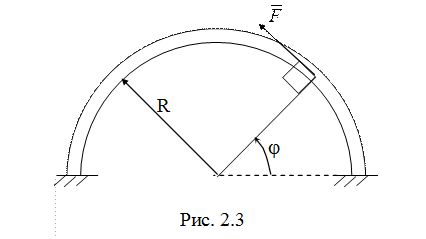
4. Тяжелая материальная
точка массы ![]() движется в вертикальной плоскости внутри гладкой тонкой неподвижной
трубки, изогнутой по дуге окружности радиуса
движется в вертикальной плоскости внутри гладкой тонкой неподвижной
трубки, изогнутой по дуге окружности радиуса ![]() (рис. 2.3). Найти зависимость силы
(рис. 2.3). Найти зависимость силы ![]() от угла
от угла ![]() , при которой давление точки на
стенки трубки отсутствует. (4 балла)
, при которой давление точки на
стенки трубки отсутствует. (4 балла)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.