Синтез и анализ обучаемой модели процесса формирования активной мощности гидроагрегата Волжской ГЭС, страница 9

С другой стороны, квадрат текущего значения амплитуды сигнала пропорционален мощности этого сигнала. Поэтому второе слагаемое определяет величину работы, затраченной за период времени  на формирование обучающего воздействия  на модель объекта управления.

Таким образом, ФОР (2.6) представляет собой аддитивную свертку двух показателей качества обучения модели объекта управления, определяющих погрешность обучения (первое слагаемое) и затраты энергии на обучение (второе слагаемое).

Весовой вклад второго слагаемого в обобщенный показатель качества обучения устанавливает параметр .

Кроме того, ФОР (2.6) определяет величину суммарной работы, затраченной на формирование сигнала рассогласования  и обучающего воздействия  за период времени обучения . Поэтому этот показатель качества управления и получил свое название: "функционал обобщенной работы".

Таким образом, задача обучения модели объекта управления эквивалентна следующей задаче условной оптимизации:

определить оценки переменных состояния и обучающее воздействие , обращающие в минимум квадратичного  ФОР (2.6) при выполнении ограничений, создаваемых уравнением состояния (2.3).

3 АЛГОРИТМ ОБУЧЕНИЯ МОДЕЛИ ПРОЦЕССА ФОРМИРОВАНИЯ АКТИВНОЙ МОЩНОСТИ

3.1 Модель системы в пространстве состояний

В данной работе использовалась модель объекта в пространстве состояний, особенности и преимущества которой рассматривались во второй главе.

В данной работе разработана модель процесса формирования активной мощности гидроагрегата, которая изображена на рисунке 10. Переменные состояния поступают в модель с измерительных устройств. Входными являются в нашем случае открытие направляющего аппарата (Z_на), угол разворота лопастей рабочего колеса (ψ_рк), напор (H), биение опор вала ротора (b) и измеренные значения вибрации (V), выходными – активная мощность (Na).

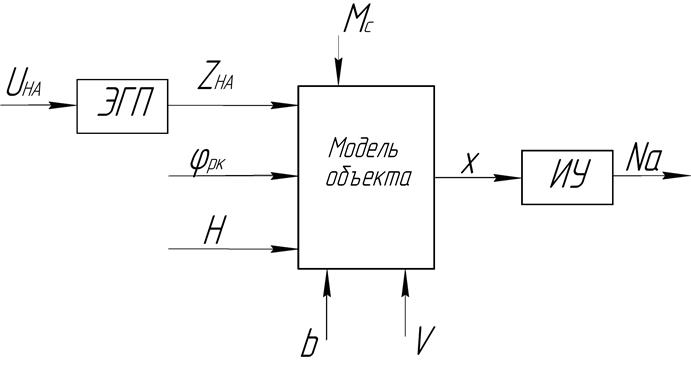
Рисунок 10 - Модель процесса формирования активной мощности

Далее составим дифференциальное уравнение I-го порядка, описывающее работу моделируемого объекта с помощью переменных состояния. Алгоритм составления модели в пространстве состояний описан подробно в главе 2.

                    ,        

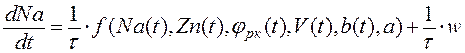где τ – постоянная времени, а w –  возмущающее воздействие. При предварительном обучении модели возмущающим воздействием будем пренебрегать.

Для моделирования на ЭВМ перейдем от дифференциального уравнения к его  разностному аналогу. Так как быстродействие современных средств вычислительной техники велико, то погрешность такого перехода будет мала.

Для этого проведем квантование времени:

,

,

,

где  - время квантования, k – количество измерений.

Время квантования Δt равно единице в нашем случае вследствие того, что датчики опрашиваются с интервалом в 1 секунду.

Заменим производную разностным выражением:

                                .                     

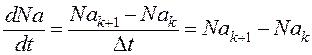Тогда (3.1) можем записать как:

                 .     

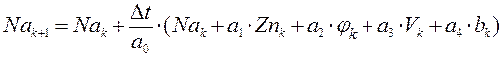Таким образом, мы получили модель объекта управления в пространстве состояний, где

вектор неизвестных параметров, которые следует определить. Для этой задачи можно применить метод наименьших квадратов.

Анализ показывает, что в гидроагрегате происходят нелинейные процессы.

Мощность гидроагрегата пропорциональна мощности, развиваемой рабочим колесом, которая потом преобразуется в генераторе в электрическую. Развиваемая мощность рабочего колеса определяется из следующего уравнения [12]:

,                                                                   (3.4)

где М – момент движущих сил,  – скорость рабочего колеса.

Момент описывается уравнением закона момента количества движения, который в данном случае описывается уравнением (3.5):

,                    (3.5)

где  – плотность воды, v₁ и v₂ – скорость во входном и выходном сечении.

На рисунке 12 построен треугольник скоростей для входа и выхода воды в гидроагрегат.

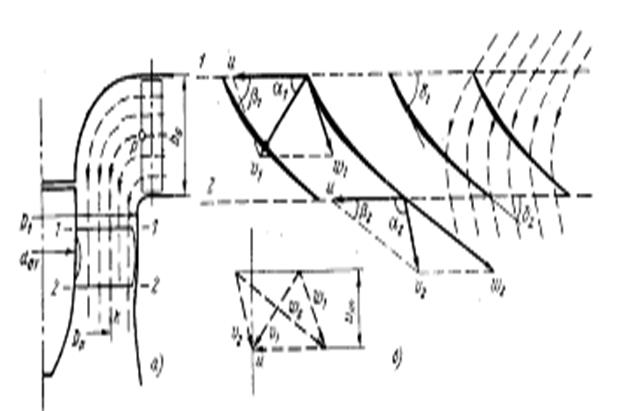
Рисунок 12 – Поток в осевой турбине

Как видно из построений, скорость зависит от напора и угла, под которым идет поток:

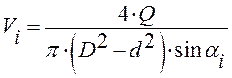.                                       (3.6)