- для аналитического конструирования обучаемой модели объекта управления и адаптивного (самонастраивающегося) регулятора (например, минимизацией соответствующих функционалов обобщенной работы с помощью принципа максимума);
- для моделирования переходных процессов в реальном времени с помощью цифровых вычислительных устройств;
- для анализа управляемости, наблюдаемости и устойчивости системы управления.
Кроме того, предполагается, что измерительные устройства имеют только случайную составляющую погрешности измерений с математическим ожиданием, равным нулю.
Применение принципов адаптации позволяет обеспечить высокую точность моделирования при существенном изменении динамических свойств изучаемой системы, унифицировать отдельные подсистемы и их блоки; сократить сроки разработки и доводки системы.
Алгоритмы управления объектом и обучения его модели можно получить, например, минимизацией соответствующих функционалов обобщенной работы с помощью принципа максимума [6]. Эти алгоритмы учитывают индивидуальные особенности объектов управления и хорошо приспособлены для реализации в цифровых системах. Схема адаптивной САУ гидроагрегатом изображена на рисунке 9.
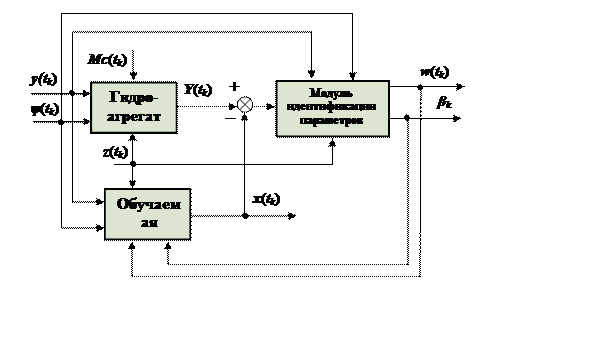
Рисунок 9 - Система обучения модели гидроагрегата
Исходные данные используют для составления математической модели объекта управления, которая в свою очередь нужна для разработки управляющего устройства. При этом выполняют предварительную обработку результатов измерений входных и выходных сигналов (исключение выбросов, восстановление пропущенных измерений, фильтрацию случайных возмущений, сглаживание и др.).
Пропущенные измерения (например, из-за исключения выбросов) восстанавливают с помощью интерполяции неизвестного закона изменения сигнала в интервалах времени между измерениями с помощью полиномов или сплайнов. В частности, можно пользоваться математическим пакетом Mathcad, который содержит интерполяционные В-сплайны.
2.2 Модель объекта управления в пространстве состояний
В цифровых системах управления используют, как правило, математическую модель объекта управления в форме "модель в пространстве состояний". Это пространство состояний образуют переменные состояния модели объекта управления [7].
Переменными состояния системы (процесса) называют минимальное количество переменных, текущие значения которых полностью определяют состояние всех элементов этой системы (процесса) в любой момент времени.
При составлении математической модели в форме "модель в пространстве состояний" объект управления рассматривают в виде системы, образованной объектом управления и измерительными устройствами, с помощью которых измеряют текущие значения части переменных состояния объекта управления. При этом в подсистему "объект " обычно включают исполнительные механизмы и другие инерционные устройства системы управления.
Модель исполнительных механизмов и объекта управления составляют в виде
системы, образованной из инерционных (динамических) звеньев 1-го порядка.
Текущие значения выходных сигналов этих звеньев полностью определяют состояние
объекта управления, поэтому они являются переменными состояния этого объекта.
Изменение состояния каждого звена описывает дифференциальное уравнение 1-го
порядка (в общем случае нелинейное), которое определяет зависимость переменной
состояния ![]() этого звена от влияющих факторов. На процессы,
происходящие в
этого звена от влияющих факторов. На процессы,
происходящие в ![]() -ом звене, оказывают влияние
управляющие воздействия
-ом звене, оказывают влияние
управляющие воздействия ![]() , другие звенья объекта
и внешняя среда в виде контролируемых (входных) воздействий
, другие звенья объекта
и внешняя среда в виде контролируемых (входных) воздействий ![]() и неконтролируемых (возмущающих) воздействий
и неконтролируемых (возмущающих) воздействий
![]() . Поэтому изменение состояния звеньев описывают
с помощью уравнений состояния:
. Поэтому изменение состояния звеньев описывают
с помощью уравнений состояния:
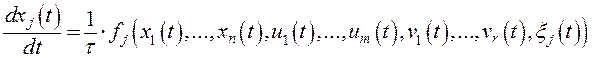 ;
; ![]() ,
,
связывающих скорости изменения переменных состояния звеньев с влияющими
факторами, где ![]() - параметр, имеющий размерность времени.
- параметр, имеющий размерность времени.
Зависимость выходных сигналов измерительных устройств ![]() от переменных состояния объекта управления
описывают с помощью статических характеристик этих измерительных устройств в
виде уравнений наблюдения:
от переменных состояния объекта управления
описывают с помощью статических характеристик этих измерительных устройств в
виде уравнений наблюдения:
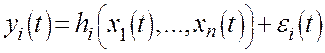 ;
; ![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.