Сопоставив (3.5) и (3.6) получим зависимость момента движущих сил от напора, а, следовательно, и открытия направляющего аппарата:
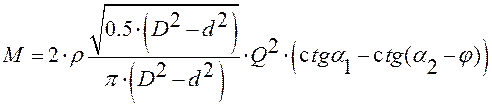. (3.7)
Согласно (3.7), момент движущих сил (и, следовательно, мощность) зависят от второй и третьей степени значения степени открытия направляющего аппарата. Третья степень получается при разложении котангенса в ряд Тейлора.
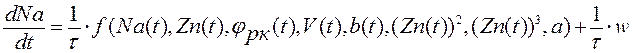. (3.8)
Составим Модель в пространстве состояний, используя разностный аналог:
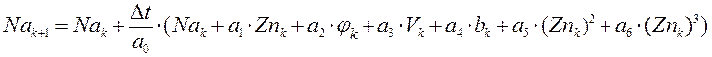. (3.9)
Таким образом, получили нелинейную модель процессов формирования активной мощности.
Предварительное обучение проводилось с помощью данных, собранных на реальных агрегатах. По результатам экспериментов выбиралась наилучшая модель.
3.2 Определение параметров модели методом наименьших квадратов
Суть и особенности метода наименьших квадратов рассмотрены в главе 2. В данной главе МНК использовался для идентификации параметров модели, полученной в прошлом разделе.
Запишем параметры модели, представленные в виде матриц, в единый массив h, а измеренную активную мощность – в виде матрицы Na:
,
,
,
,
,
Составим функцию штрафа по невязке измеренного сигнала и сигнала модели:
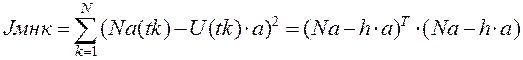. (3.10)
Из необходимого и достаточного условия минимума квадратичной функции штрафа
(3.4) получим алгоритм идентификации
параметров ai:
. (3.11)
Для нелинейной модели в матрицу h добавляются соответствующие столбцы, алгоритм остается прежним. Листинг алгоритма, реализованного в пакете программ Mathcad приведен в приложении А.
Таким образом, составлен алгоритм предварительного обучения модели процесса формирования активной мощности в пространстве состояний с помощью метода наименьших квадратов. Числовые значения будут получены во время эксперимента в главе 4.
3.3 Рекуррентный алгоритм МНК
Для обучения модели в реальном времени и учета средней погрешности можно использовать рекуррентный метод наименьших квадратов (РМНК), который имеет ряд преимуществ перед традиционным МНК. РМНК, в отличии от МНК, пересчитывает параметры модели с использованием предыдущих значений и добавлении поправки на каждом шаге. В МНК же на каждом шаге пересчитывается вся матрица значений, то есть использовать этот алгоритм в оперативном режиме для систем управления крайне неудобно, так как тратится вычислительная мощность и возможны ошибки из-за плохо обусловленных матриц.
Алгоритм и особенности рекуррентного метода наименьших квадратов описаны в главе 2.
Составим функционал обобщенной работы для модели процесса формирования активной мощности:
 |
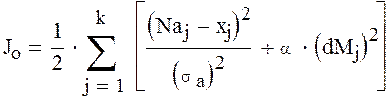. (3.12)
Задавались начальные значения для активной мощности Na1, средней погрешности dM, членов уравнения Риккати, параметра регуляризации α:
Эти значения требовались для последующих вычислений уравнения Риккати, значений активной мощности и возмущающего воздействия.
Далее вычислялись значения мощности и возмущающего воздействия в цикле по k.
Листинг алгоритма, реализованного в пакете программ Mathcad представлен в приложении Б.
Таким образом, получили алгоритм для обучения модели в оперативном режиме с вычислением среднего возмущающего воздействия.
3.4 Модель электрогидравлического преобразователя
Для дальнейшей работы понадобится модель системы электрогидравлического преобразователя (ЭГП).
Устройство ЭГП и его структурная схема представлены на рисунках 13 и 14.
Управляющее воздействие в виде электрического сигнала поступает в ЭГП и заставляет двигаться подпружиненный постоянный магнит 1. Тот, в свою очередь, двигает золотник 2, регулирующий вход-выход масла. Таким образом, меняются между собой области высокого и низкого давления, что вызывает перемещение поршня 3. Через систему механизмов поршень изменяет угол разворота лопаток РК (рабочего колеса). Контур охвачен обратными связями, т.е. является следящей системой.
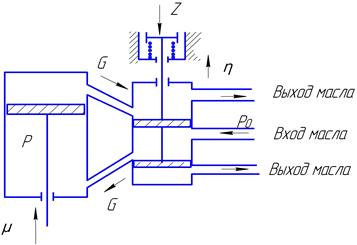
Рисунок 13 - Электрогидравлический преобразователь
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.