Синтез и анализ обучаемой модели процесса формирования активной мощности гидроагрегата Волжской ГЭС, страница 8

где  - погрешность измерений -го измерительного устройства.

Математическая модель объекта управления в форме "модель в пространстве состояний" включает в себя систему уравнений состояния (2.1) (в виде дифференциальных уравнений первого порядка) и систему уравнений наблюдения (2.2) (в виде алгебраических уравнений, связывающих выходные сигналы измерительных устройств с переменными состояния).

Математическую модель процесса формирования активной мощности в пространстве состояний обычно представляют в матричной форме. Для этого переменные состояния  объединяют в вектор переменных состояния объекта управления:

.

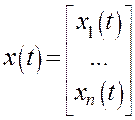В ходе работы были составлены несколько альтернативных моделей, линейных и нелинейных (в главе 3).

Для использования модели в дискретных системах перейдем к разностному аналогу, так как для современных цифровых систем, обладающих высокой скоростью дискретизации,  такой переход не внесет большой погрешности [8].

,

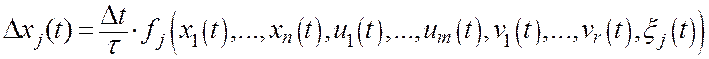где - параметр, имеющий размерность времени.

Таким образом, мы получили модель объекта управления, пригодную для использования в цифровой системе управления, однако требуется определить постоянные параметры модели, то есть провести предварительное обучение.

2.3 Идентификация постоянных параметров модели объекта управления

Все методы оценивания параметров, так или  иначе, опираются на метод наименьших квадратов и рассматривают оценку как идентификацию параметров. Поэтому идентификацию параметров модели проведем с помощью метода наименьших квадратов.

Суть метода заключается в минимизации функции штрафа, представляющей собой квадрат сигнала разсоглосования между измеренным значением величины и значения, полученного по модели. То есть, функционал характеризует собой ошибку прогноза модели и эту ошибку минимизируют с помощью принципа максимума.

Составим функцию штрафа метода наименьших квадратов (МНК):

,         

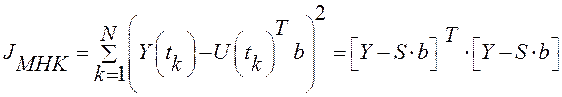где используются следующие векторы и матрица :

;  ;  ;   ,

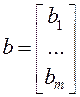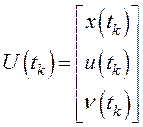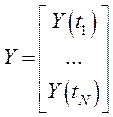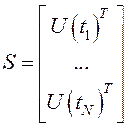Y(t_k) – измеренные значения реального параметра.

Из необходимого и достаточного условия минимума квадратичной функции штрафа  получим алгоритм идентификации параметров :

                    .                                            

Метод наименьших квадратов обеспечивает состоятельные оценки параметров при любых законах распределения возмущающих воздействий [9].

Таким образом, мы получили модель процесса и постоянные параметры модели, то есть провели предварительное обучение модели, которая нам понадобилась для алгоритма обучения модели объекта управления в оперативном режиме.

2.4 Алгоритм обучения модели объекта управления

Обучение модели будем проводить с помощью рекуррентного метода наименьших квадратов, который имеет ряд преимуществ по сравнению с традиционным (одношаговым) методом. РМНК использует оценки, вычисленные на предыдущем шаге, в отличии от МНК, который обрабатывает весь массив данных каждый раз. Матрица Гессе может быть плохо обусловлена, что приведет к большой погрешности оценивания параметров модели процесса. РМНК экономит математические ресурсы, а главное время, что позволяет создавать модель, которая будет отслеживать изменение параметров во времени, т.е. позволит создать обучающуюся модель.

Алгоритм РМНК состоит в минимизации функционала обобщенной работы, который определяет качество обучения модели объекта управления[10]:

,        

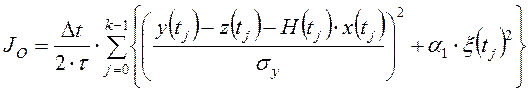где:  - нормирующий множитель (предел основной погрешности измерений выходного сигнала объекта управления );  - весовой коэффициент (параметр регуляризации), величину которого выбирают из диапазона .

Функционалу обобщенной работы (2.6) можно дать следующую физическую трактовку [11]:

Сигнал  поступает на вход модели объекта управления. От его величины зависит величина выходного сигнала модели объекта , поэтому сигнал  можно использовать для  управления (обучения) модели объекта управления.

Числитель первого слагаемого ФОР - это текущее значение сигнала рассогласования

между выходным сигналом  реального объекта  и выходным сигналом  модели этого объекта. Поэтому первое слагаемое определяет величину погрешности обучения модели за период времени : квадрат среднеквадратического отклонения сигнала рассогласования.