Задачи и системы адаптивного управления, страница 9

В классической теории автоматического управления применяют линейную модель объекта управления в отклонениях от установившегося (номинального) режима работы системы управления. Однако такая модель гарантирует требуемое качество управления только в небольшой окрестности этого установившегося режима работы системы управления. Для многорежимных объектов нужно применять разные модели для разных режимов работы.

В цифровых системах управления обычно применяют линейную модель объекта управления в отклонениях от опорной траектории. При составлении такой модели непрерывные процессы в объекте управления описывают разностными аналогами уравнений (8), (9). Для этого выполняют квантование сигналов и переменных состояния во времени и по уровню. Наиболее часто разностную модель получают с помощью амплитудной модуляции (АМ).

В этом случае формируют дискретные моменты времени , отстоящие друг от друга на постоянную величину (шаг квантования времени) :

,    .

В текущий момент времени  известны значения переменных состояния объекта управления  и управляющих  воздействий в предшествующий момент времени . Поэтому вектор скоростей изменения переменных состояния в текущий момент времени  можно заменить разностным аналогом:

.

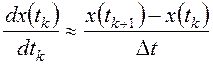В -мерном пространстве состояний значения переменных состояния объекта управления , , …,  образуют точки годографа вектора  (опорные точки перемещения объекта управления в пространстве состояний). В интервале  времени функцию, стоящую в правой части уравнения (8), разложим в ряд Тейлора в окрестности опорной точки .  При небольшом шаге квантования времени (с.) в этом разложении можно оставить только линейные слагаемые, так как остальные члены ряда будут пренебрежимо малы по сравнению с первым членом ряда. В этом случае получим следующий усеченный ряд Тейлора:

,

где:

;

;

;

.

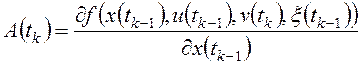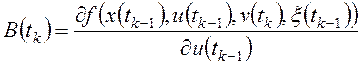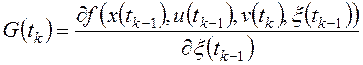При подстановке этих формул в уравнение (8) получим линейное разностное уравнение состояния объекта управления:

 Линейное разностное уравнение наблюдения

где:

;  ,

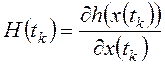получают разложением функции  в ряд Тейлора в окрестности опорной точки  в пространстве состояний объекта управления (при изменении времени в интервале ).

Последовательно перемещаясь из опорной точки  в момент времени  в опорную точку  в следующий момент времени  (где ), можно с помощью уравнений (10), (11) обеспечить   требуемую точность моделирования процессов, происходящих в объекте управления в течение всего времени работы системы управления (за счет выбора достаточно маленькой величины шага квантования времени ).

4.1.  Модель в пространстве состояний процесса изменения уровня в барабане котла системы подготовки перегретого пара.

Преобразуем уравнения (1), (2), (6) модели объекта управления к стандартному виду "модель в пространстве состояний".

Для этого составим вектор переменных состояния объекта управления и матрицы:

;   ;    ;

;      .   

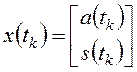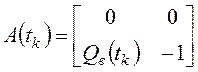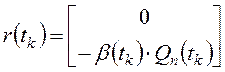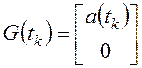В матричной форме записи уравнения (2) и (6) образуют уравнение состояния:

а уравнение (5.1) - уравнение наблюдения:

Кроме того, в математическое описание объекта управления входят уравнения (3) и (4), определяющее зависимость расхода питательной воды  от величины управляющего воздействия , и уравнение (5), которое нужно учитывать в системе управления уровнем в качестве ограничения.

Уравнение наблюдения (11) описывает количественную зависимость выходных сигналов измерительных устройств (датчиков) от текущих значений переменных состояния.

 Уравнение состояния (10) описывает количественную зависимость текущих значений переменных состояния от значений этих переменных в предыдущий момент времени и от входных воздействий (управляющих воздействий, измеряемых  входных воздействий и неконтролируемых возмущающих воздействий).