Задачи и системы адаптивного управления, страница 11

4.4.   Алгоритм обучения модели объекта управления

Функционал обобщенной работы. Качество обучения модели объекта управления(10), (11) определяет скалярный показатель (функционал обобщенной работы) [23]:

+ ,

(14)

где:  - нормирующий множитель (предел основной погрешности измерений выходного сигнала объекта управления );  - весовой коэффициент (параметр регуляризации), величину которого выбирают из диапазона ;

.

Функционалу обобщенной работы (14) можно дать следующую физическую трактовку [20]:

     Сигнал  поступает на вход модели объекта управления. От его величины зависит величина выходного сигнала модели объекта , поэтому сигнал  можно использовать для  управления (обучения) модели объекта управления.

     Числитель первого слагаемого ФОР - это текущее значение сигнала рассогласования

между выходным сигналом  измерительного устройства и выходным сигналом  модели этого измерительного устройства. Поэтому первое слагаемое определяет величину погрешности обучения модели за период времени : квадрат среднеквадратического отклонения сигнала рассогласования.

      С другой стороны, квадрат текущего значения амплитуды сигнала пропорционален мощности этого сигнала. Поэтому второе слагаемое определяет величину работы, затраченной за период времени  на формирование обучающего воздействия  на модель объекта управления.

      Таким образом, ФОР (14) представляет собой аддитивную свертку двух показателей качества обучения модели объекта управления, определяющих погрешность обучения (первое слагаемое) и затраты энергии на обучение (второе слагаемое).

      Весовой вклад второго слагаемого в обобщенный показатель качества обучения устанавливает параметр .

       Кроме того, ФОР (14) определяет величину суммарной работы, затраченной на формирование сигнала рассогласования  и обучающего воздействия  за период времени обучения . Поэтому этот показатель качества управления и получил свое название: "функционал обобщенной работы".

Таким образом, задача обучения модели объекта управления эквивалентна следующей задаче условной оптимизации:

определить оценки переменных состояния и обучающее воздействие , обращающие в минимум квадратичный  ФОР (14) при выполнении ограничений, создаваемых уравнением состояния (10).

Рекуррентный алгоритм обучения модели объекта управления. Задачу оптимизацииквадратичного ФОР (14) с ограничениями, создаваемыми разностным уравнением состояния (10) (задача условной оптимизации), решают с помощью принципа максимума в следующей  последовательности [23]:

1). С помощью вектора неопределенных множителей Лагранжа  преобразуют задачу условной оптимизации квадратичного ФОР (14) с ограничениями (10) в задачу безусловной оптимизации функции Гамильтона, которую формируют по алгоритму:

.

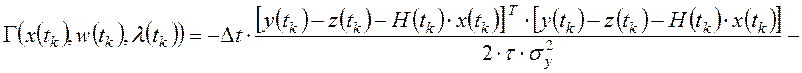
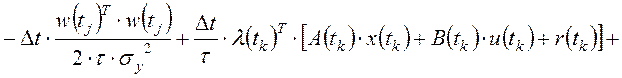
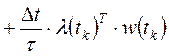2). Из необходимых и достаточных условий минимума функции Гамильтона получают уравнения Эйлера-Лагранжа:

;

;

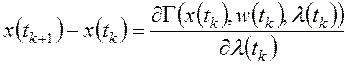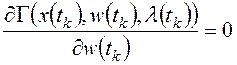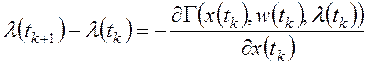
и краевые условия в начальный  и  конечный   моменты времени:

;  .

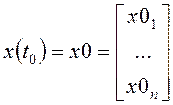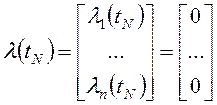3). С помощью инвариантного погружения двухточечной краевой задачи, полученной в п. 2, составляют уравнения рекуррентного алгоритма обучения модели объекта управления (вычисления текущих значений переменных состояния в моменты времени ):

;   ;   ;

;

    

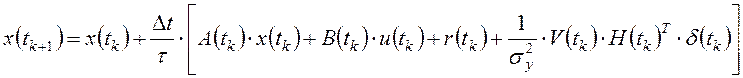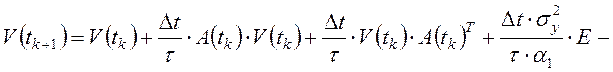
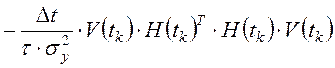
с начальными условиями

   ;   ,

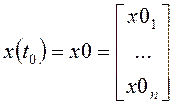где  - единичная матрица.

Текущие значения переменных состояния модели (12), (13) многомерного объекта управления, обращающие в минимум ФОР (14), где , вычисляют с помощью рекуррентного алгоритма:

;    ;     , с начальными условиями ;    .

(15)

Анализ алгоритма обучения. Р. Калман с помощью метода Ляпунова доказал, что система (15) устойчива, если объект управления (10), (11) управляем и наблюдаем [10].

Для выяснения других свойств обучаемой модели объекта управления (15) первое уравнение алгоритма (15) с помощью формул (6) преобразуем в систему следующих скалярных уравнений:

;                                            

               .                                                     

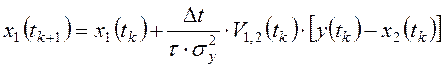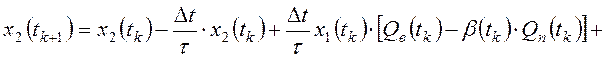
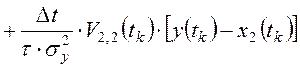По условию несмещенности выходной сигнал обученной модели  должен совпадать с выходным сигналом объекта управления :