Задачи и системы адаптивного управления, страница 12

.                                                            

Из сравнения уравнения (2) и полученных скалярных уравнений видно, что равенство  достигается только при выполнении условия:

.     

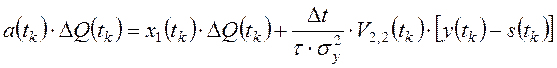Из этого условия в свою очередь следует алгоритм вычисления текущего значения параметра :

.                                          

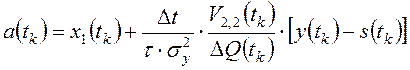С учетом этих результатов алгоритм (15) можно представить в следующем виде:

;     ;    ;    ;            , где: ; ;                   ;        ; ;      .

(16)

 Схема системы, реализующей алгоритм (16), изображена на рис. 9.

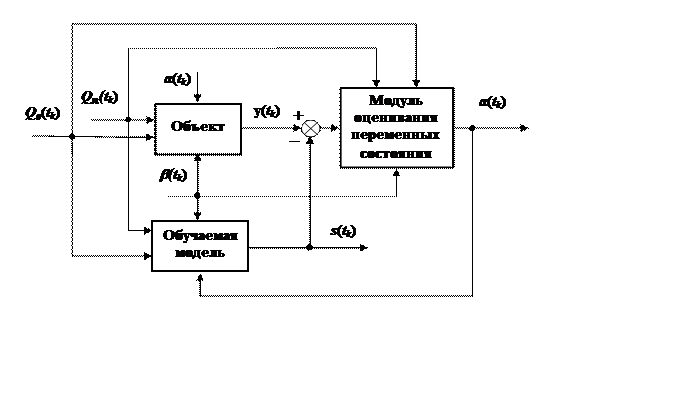
Рис. 9.  Система обучения модели процесса изменения

уровня пароводяной смеси в барабане котла

Из уравнений (16) видно, что оценку текущего значения параметра  система обучения формирует с помощью ПИ-регулятора с переменными параметрами  и .

5. Разработка алгоритма управления технологическим процессом

5.1. Модель разомкнутой системы управления в пространстве состояний

Алгоритм управления разрабатывают с использованием математического описания в пространстве состояний элементов цифровой системы управления.

Математическая модель  процесса изменения уровня пароводяной смеси в барабане котла (рис. 7) включает:

- уравнение состояния объекта управления (2);

- уравнения (3), (4) связывающие выходной сигнал расходомера питательной воды  с управляющим воздействием ;

Для математического описания системы управления нужно составить модель регулятора и задание регулятору (в виде уравнений требуемой (желаемой) траектории изменения управляемой переменной во времени и дополнительных ограничений).

Априорная модель регулятора. Разрабатываемая система управления должна обеспечивать равенство нулю статической погрешности управления. Из теории автоматического управления известно, что для этого регулятор должен содержать интегрирующее звено. Поэтому для формирования управляющего воздействия можно применить линейную динамическую систему, состояние которой описывает следующая система разностных уравнений:

; ;        ,

(17)

где ,  - входные сигналы регулятора, подлежащие определению.

Формирование задания регулятору. Пусть известны:

- требуемое значение управляемой переменной в установившемся режиме работы системы управления ;

- время регулирования ;

- допустимая погрешность регулирования .

Тогда требуемые значения управляемой переменной в процессе управления можно задать с помощью уравнения:

.

В дальнейшем будем считать, что требуемые значения управляемой переменной  известны. Тогда траекторию изменения управляемой переменной в процессе управления определяет уравнение:

,

(18)

где  - погрешность управления.

В системе подготовки перегретого пара используют ограничение в форме равенства (5), которое совместно с уравнениями (3) и (4) определяет связь расхода перегретого пара  из котла с управляющим воздействием :

,

19)

где

;         .

(20)

Таким образом, с помощью уравнений (17)-(20) системе управления задают требуемые (желаемые) законы изменения переменной состояния объекта управления  и переменной состояния регулятора .

Модель разомкнутой системы управления в пространстве состояний. Составим вектор переменных состояния системы управления

и представим уравнения (2), (3), (17)-(20) модели разомкнутой системы управления в стандартном виде "модель в пространстве состояний":

;	(21)
,	(22)

где:

;        ; ;         ; .

Полученная модель системы управления содержит уравнение состояния (21) и уравнение (22), определяющее дополнительное ограничение на переменные состояния системы управления (задание системе управления).

Система (21), 22) имеет две переменные состояния. Матрица управляемости  этой системы по входу  имеет ранг , а матрица наблюдаемости  имеет ранг . Поэтому модель системы управления (21), (22) наблюдаема и управляема по входу .