Задачи и системы адаптивного управления, страница 10

Следует отметить, что уравнение состояния (10) учитывает действие всех влияющих факторов на переменные состояния, в том числе, и взаимное влияние разных переменных состояния друг на друга. С помощью модели в пространстве состояний, представленной в матричной форме уравнениями (10), (11),  можно моделировать процессы, происходящие как в одноконтурных системах управления с одним входом и одним выходом, так и в многоконтурных (многомерных) системах управления с перекрестными связями. Поэтому анализ и синтез различных систем управления (одномерных и многомерных, линейных и нелинейных) можно выполнять с помощью одинаковых алгоритмов.

Математическая модель объекта управления (10), (11),  может  содержать неизвестные параметры и возмущающие воздействия, которые необходимо определять в процессе управления (обучать модель).

Задача обучения модели многомерного объекта управления имеет решение, если эта система управляема по входу, на который подается неконтролируемое возмущающее воздействие , и наблюдаема, а возмущающее воздействие  является сигналом  с ограниченной энергией [23].

4.2. Анализ управляемости и наблюдаемости модели объекта управления

Анализ управляемости. Для анализа управляемости системы необходимо составить матрицу управляемости, вычислить (например, с помощью пакета прикладных программ Mathcad) ранг этой матрицы и сравнить его с числом переменных состояния.

Модель (12), (13) процесса изменения уровня пароводяной смеси в барабане котла имеет число переменных состояния .

Составим для этой системы матрицу управляемости по входу :

.

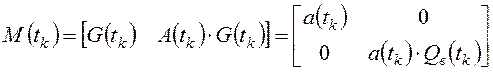Эта матрица имеет ранг , поэтому динамическая система (12), (13)  управляема по входу .

Анализ наблюдаемости. Систему называют наблюдаемой, если все ее переменные состояния можно определить по результатам измерений выходных сигналов, выполненных в ограниченном промежутке времени.

Для анализа наблюдаемости необходимо составить  матрицу наблюдаемости и сравнить (например, с помощью пакета прикладных программ Mathcad) ранг этой матрицы с числом переменных состояния системы.

Для динамической системы (12), (13), которая имеет число переменных состояния , матрица наблюдаемости

.

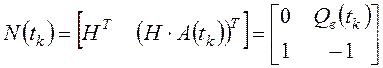Ранг этой матрицы , следовательно, динамическая система (12), (13) наблюдаема.

Таким образом, модель объекта управления (12), (13) наблюдаема и управляема по входу . Поэтому можно по результатам измерений сигналов ,  и  определить текущие значения возмущающего воздействия  и параметра , которые изменяются в процессе работы системы подготовки перегретого пара.

4.3.   Идентификация постоянных параметров модели объекта           управления

Алгоритм идентификации параметров модели (4) процесса изменения расхода питательной воды. Составим функцию штрафа метода наименьших квадратов (МНК):

где используются следующие векторы и матрица :

;    ;   ;   .                  

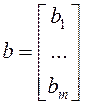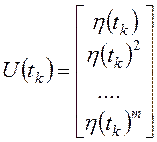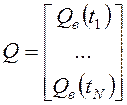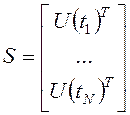Из необходимого и достаточного условия минимума квадратичной функции штрафа  получим алгоритм идентификации параметров :

Алгоритм идентификации параметров уравнения состояния. Для идентификации постоянной времени  и начальной оценки  переменного параметра  преобразуем уравнения (1), (2) и (5) к следующему виду (в предположении, что ,  и ):

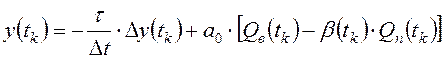
 Составим функцию штрафа МНК:

где:

 ;       ;                                                  

;         ;

.

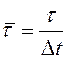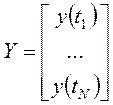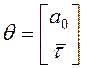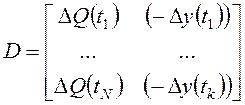Из необходимого и достаточного условия минимума функции штрафа  получим алгоритм идентификации параметров:

Анализ алгоритма идентификации. Метод наименьших квадратов обеспечивает состоятельные оценки параметров при любых законах распределения возмущающих воздействий [12].

Следовательно, допустимую погрешность идентификации можно обеспечить за счет выбора протяженности  используемого скользящего временного окна.

Полученные алгоритмы идентификации  параметров модели объекта управления  предусматривают обращение  матриц:  и . Это возможно, если выполняются условия:

;    ,

которые и являются необходимыми условиями идентифицируемости параметров модели объекта управления.

Таким образом, при анализе эффективности применяемого алгоритма идентификации параметров нужно проверять выполнение условий идентифицируемости и состоятельности получаемых оценок этих параметров.