Задачи и системы адаптивного управления, страница 4

В условиях априорной неопределенности для управления объектами широко применяются системы с непрямым адаптивным управлением, так как они позволяют обеспечить высокое качество функционирования. Основ­ным звеном таких систем является блок идентификации. В зависимости от свойств объекта и требований, предъявляемых к системе, могут приме­няться как методы ретроспективной, стратегической идентификации (модель определяется вне контура управления), так и подходы, основанные на текущей или оперативной идентификации [9]-[15]. Несмотря на обилие публикаций можно выделить лишь несколько подходов к адаптивному параметрическому оцениванию. В основном это методы наименьших квадратов, стохастической аппроксимации и их модифика­ции, а также различные градиентные алгоритмы. При решении практиче­ских задач теории управления теоретические предпосылки, лежащие в ос­нове указанных методов, как правило, не выполнялись. Поэтому эффективность многих процедур идентификации была низкой. В частности, терялось свойство оптимальности, снижалась скорость сходимости [11]. Поэтому в теории идентификации возникла проблема обеспечения грубости применяе­мых алгоритмов и методов, непосредственно связанная с учетом ограни­чений и условий функционирования системы «объект + среда». Это был следующий этап развития статистических методов параметрического оценивания. Для решения проблемы робастности (гру­бости) адаптивных алгоритмов было предложено ряд подходов [11], [15], которые в последующем составили основу нового научного направления - информационной теории идентификации. Указанное на­правление базировалось на учете априорной информации о среде в виде за­дания класса наименее благоприятных распределений помехи. Однако и такой подход не позволяет полностью учесть реальные условия функционирования объ­екта. Возникают трудности, связанные с оценкой качества работы алгоритмов идентификации по конечным выборкам. Полу­ченные алгоритмы являются нелинейными относительно ошибки оценива­ния. Но если ограничения на помеху нестационарные, или заданы дополнительные ограничения в форме неравенств, то этот подход неработоспособен [11].

Кроме того, в реальных ситуациях в адаптивных системах автоматического управления можно использовать лишь одну реализацию возмущающих воздействий, которые являются ограниченными по абсолютной величине функциями времени. Поэтому традиционные адаптивные системы автоматического управления неизбежно имеют статическую погрешность регулирования и создают существенное перерегулирование управляемых переменных.

При отказе от статисти­ческой трактовки возмущающих воздействий и погрешностей измерений применяют адаптивные системы управления с обучаемой моделью объекта управления (рис. 1). Они различаются методами получения оценок возмущающих воздействий и параметров объекта [14]-[20]. Эти методы направлены на получение множественных оценок параметров объекта вида , содержащих истинные значения искомого вектора параметров, где  пред­ставляет собой некоторое априори неизвестное ограниченное множество, которое определяют в процессе идентификации. Получаемые в этом случае оценки принято называть гарантированными.

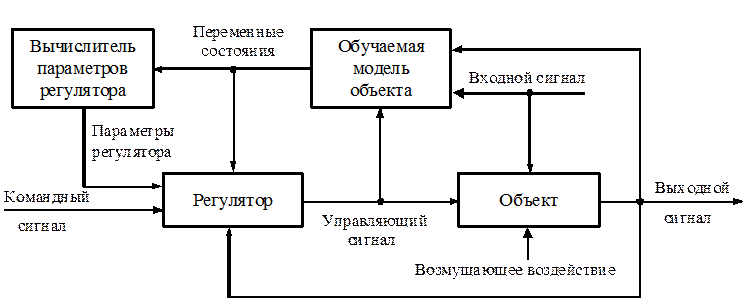
Рис. 1. Адаптивная система управления с обучаемой моделью

Алгоритмы управления объектом и обучения его модели можно получить, например, минимизацией соответствующих функционалов обобщенной работы с помощью принципа максимума. Эти алгоритмы учитывают индивидуальные особенности объектов управления и хорошо приспособлены для реализации в цифровых системах.

2.  Постановка задачи адаптивного управления уровнем пароводяной среды в барабане котла

Для регулирования уровня пароводяной среды в барабане котла системы подготовки перегретого пара применяют систему управления с компенсацией возмущения (рис. 2) с жесткой (постоянной) настройкой параметров регулятора [21].

На вход регулятора уровня подается взвешенная сумма сигналов, определяющих текущие значения уровня пароводяной смеси в барабане  (основной регулируемой величины), расхода питательной воды  (вспомогательной переменной состояния объекта управления) и расхода перегретого пара из котла  (контролируемого влияющего фактора). Значения весовых коэффициентов устанавливаются в блоке коррекции вспомогательной переменной (БК) и в блоке компенсации возмущения (КВ), вносимого влияющим фактором.